Notation and Set Theory
Sets are the most basic building blocks in mathematics, and it is in fact
not easy to give a precise definition of the mathematical object set.
Once sets are introduced, however, one can compare them, define operations
similar to addition and multiplication on them, and use them to define new
objects such as various kinds of number systems. In fact, most of the topics in
modern analysis are ultimately based on sets.
Therefore, it is good to have a basic understanding of sets, and we will
review a few elementary facts in this section. Most, if not all, of this section
should be familiar and its main purpose is to define the basic notation so that
there will be no confusion in the remainder of this text.
Definition: Sets and Operations on Sets
- A set is a collection of objects chosen from some universe. The
universe is usually understood from the context. Sets are denoted by
capital, bold letters or curly brackets.
- A
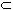 B:
A is a subset of B means that every element in A
is also contained in B. B:
A is a subset of B means that every element in A
is also contained in B.
- A
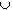 B:
A union B is the set of all elements that are either in A or
in B or in both. B:
A union B is the set of all elements that are either in A or
in B or in both.
- A
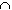 B:
A intersection B is the set of all elements that are in both sets
A and B. B:
A intersection B is the set of all elements that are in both sets
A and B.
- A \ B: A minus B are all elements from A that are
not in B.
- comp(A): The complement of A consists of all
elements that are not in A.
- Two sets are disjoint if A
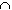 B
= 0 (the empty set) B
= 0 (the empty set)
- Two sets A and B are equal if A
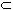 B
and B B
and B
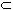 A A
The most commonly used sets are the sets of natural numbers,
integers, rational and real numbers, and the empty set.
They are usually denoted by these symbols:
- N = {1, 2, 3, 4, ... } = natural numbers (sometimes 0 is
considered part of the natural numbers as well)
- Z = {... -3, -2, -1, 0, 1, 2, 3, ... } = integers
- Q = {p / q : p, q
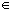 Z}
(read as �all number p / q, such that p and q are elements of Z) =
rational numbers Z}
(read as �all number p / q, such that p and q are elements of Z) =
rational numbers
- R = real numbers
- 0 = empty set (the set that contains no elements)
All of the number systems (except the natural numbers) will be defined in a
mathematically precise way in later sections. First, some examples:
Examples:
- Define the following sets: E = { x: x = 2n for n
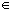 N},
O = { x: x = 2n + 1 for n N},
O = { x: x = 2n + 1 for n
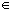 N},
A = { x N},
A = { x
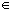 R
: -4 < x < 3}, B = { x R
: -4 < x < 3}, B = { x
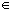 R
: -1 < x < 7}, and I = { x R
: -1 < x < 7}, and I = { x
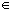 R:
x2 = -2}. Then: R:
x2 = -2}. Then:
-
What, in words, are the sets E, O, and I ?
-
Find A
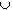 B,
A B,
A
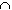 B,
A \ B, comp(A). B,
A \ B, comp(A).
-
Find O
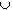 E,
O E,
O
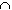 I,
comp(I). I,
comp(I).
Sets can be combined using the above operations much like adding and
multiplying numbers. Familiar laws such as associative, commutative, and
distributive laws will be true for sets as well. As an example, the next result
will illustrate the distributive law; other laws are left as exercises.
Proposition: Distributive Law for Sets
- A
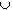 (B (B
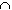 C)
= (A C)
= (A
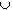 B) B)
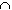 (A (A
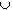 C) C)
- A
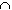 (B (B
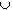 C)
= (A C)
= (A
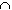 B) B)
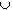 (A (A
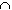 C) C)
Many results in set theory can be illustrated using Venn diagram, as in the
above proof. However, such diagrams do not represent mathematically rigorous
proofs. Nonetheless, before an actual proof is developed, it is first necessary
to form a mental picture of the assumptions, conclusions, and implications of a
theorem. For this process a Venn diagram can be very helpful. You can practice
Venn diagrams by using them for some of the true/false statements in the
exercises.
There are many other theorems dealing with operation on sets. One that is
particularly interesting is the theorem about de Morgan's Laws, because it deals
with any number of sets (even infinitely many). Drawing a Venn diagram in such a
situation would be impossible, but a mathematical proof can easily deal with
this situation:
Theorem: de Morgan�s Laws
-
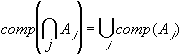 i.e. the complement of the intersection of any number of sets equals the
union of their complements.
i.e. the complement of the intersection of any number of sets equals the
union of their complements.
-
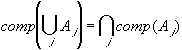 i.e. the complement of the union of any number of sets equals the
intersection of their complements.
i.e. the complement of the union of any number of sets equals the
intersection of their complements.
So far, we have reviewed a few basic facts from set theory, and also got an
idea about how a course in Real Analysis will proceed:
First, there are definitions, stating precisely what we are talking about.
From those definitions we derive new results, based on old results, notation,
and logic. The new results are called Theorems (if they are important or
broad), Propositions (if they are interesting, but not so broadly
applicable) and Corollaries (which are usually restatements of theorems
or propositions in special situations). We will proceed that way throughout the
text.
The most difficult part of Real Analysis is trying to understand the proofs
of new results, or even developing your own proofs. While there are a few
'general' methods for proofs, a lot of experience and practice is needed before
you will feel familiar with giving your own proofs. However, only a few proofs
require real ingenuity, and many other proofs can be understood by carefully
reviewing the definitions of terms involved. Therefore, as a rule:
- write down the precise mathematical definitions of all terms involved
before starting a proof
In following that rule, one often gets ideas about how to start a proof by
starting to manipulate the mathematical symbols involved in the precise
definitions of the terms.
Keep in mind that a proof can (almost) never be given by means of examples.
Working out a few examples can certainly be helpful - and should in fact always
be done before starting a proof - but they can not constitute a rigorous proof
of a general statement.
Two types of proofs will be encountered frequently, and deserve special
attention:
- Proof by Induction: This type of proof is introduced in detail in
the next chapter.
- Proof by Contradiction: In this type of proof one assumes that
the proposition (i.e. what one actually would like to proof) is false. Then
one derives a contradiction, i.e. a logical impossibility. If that can be
accomplished, then one has shown that the negation of a statement will
result in an illogical situation. Hence, the original statement must be
true.
Examples:
-
Prove that when two even integers are multiplied, the result is an even
integer, and when two odd integers are multiplied, the result is an odd
integer.
-
Prove that if the square of a number is an even integer, then the original
number must also be an even integer. (Try a proof by contradiction)
-
Euclid's Theorem states that there is no largest prime. A proof by
contradiction would start out by assuming that the statement is false, i.e.
there is a largest prime. The advantage now is that if there was a largest
prime, there would be only finitely many primes. This seems easier to handle
than the original statement which implies the existence of infinitely many
primes. Finish the proof.
|

