What is topology?
Topologists are mathematicians who study qualitative questions about
geometrical structures. We do not ask: how big is it? but rather: does it have
any holes in it? is it all connected together, or can it be separated into
parts? A commonly cited example is the London Underground map.
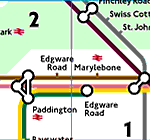
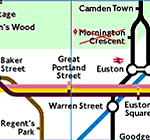
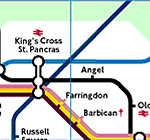
This will not reliably tell you how far it is from Kings Cross to Picadilly,
or even the compass direction from one to the other; but it will tell you how
the lines connect up between them. In other words, it gives topological rather
than geometric information. Again, consider a doughnut and a teacup, both made
of BluTack. We can take one of these and transform it into the other by
stretching and squeezing, without tearing the BluTack or sticking together bits
which were previously separate. It follows that there is no topological
difference between the two objects. Consider the problem of building a fusion
reactor which confines a plasma by a magnetic field.
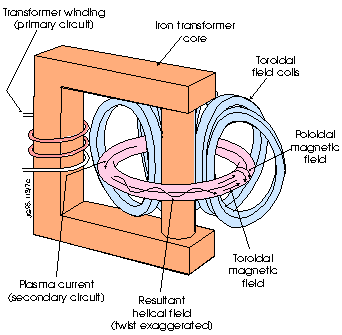
Imagine a closed surface surrounding the plasma. At each point on the
surface, the component of the magnetic field parallel to the surface must be
nonzero, or the plasma will leak out. We are thus led to the following question:
given a surface S, is it possible for there to be a field of vectors tangent at
each point of S which is nowhere zero? It turns out that this depends solely on
the topological nature of S. If S is the surface of a sphere, it is not
possible. Magnetic confinement of a ball of plasma just does not work. The only
type of surface for which this approach is possible is the inner tube shape,
which is of course the solution universally used for such reactors. (I do not
claim that engineers needed topologists to point this out; on the contrary, this
is a nice example precisely because many people can see for themselves that the
claim is true.) Another amusing consequence of the same argument is that at any
given time, some point on the Earth's surface is windless.

While these examples are interesting, they are somewhat limited.
Topologically speaking there are few possibilities for solid objects;
essentially the only variable is the number of holes. Interesting things happen,
however, when we work with abstract objects in more than three dimensions. This
is not the dry academic game that it might appear at first sight. Consider the
ubiquitous use of graphs in science. One often sees graphs of (say) pressure
against temperature. Neither variable is naturally a geometric quantity.
Nonetheless, they can be represented by distances on a sheet of paper. Moreover,
geometric concepts such as slopes of lines and areas of regions can usefully be
interpreted in terms of thermodynamics. In principle, none of these geometric
ideas are neccessary; all the arguments can be carried through algebraically
without any diagrams. Nonetheless, most of us find diagrams helpful and
illuminating, because we have a better intuitive feel for geometry than for
algebra. Now suppose that instead of two variables (pressure and temperature) we
are faced with a problem involving five or six. We might like to draw a six
dimensional graph, but we do not have enough space. We can try to imagine what
six dimensional geometry might be like, but it is difficult to have confidence
in our intuition about such a theoretical construct so far removed from
experience. On the other hand, we can try to do the problem by pure algebra, but
in doing so we forgo the visual insight which is one of the most powerful
faculties of the human mind. In fact, mathematicians have developed a rather
strange yet highly fruitful approach to such problems. The questions addressed
are officially formulated in terms of logic and algebra rather than geometry,
and solutions are required to be expressed in such terms. Where geometrical
concepts are used, they must be defined in terms of algebraic ones. All use of
such concepts is to be justified purely in terms of such definitions, rather
than in terms of geometric intuition. The visual imagination guides the course
of the argument, and suggests what one should try to prove, but the argument
must stand in its own right. There is an interesting, if limited, analogy with
physical science, with rigorous proof playing the role of experiment and
geometrical speculation (amongst other things) that of the more mysterious
processes by which new theories emerge. Let us consider an example with more
than three dimensions. Imagine an industrial robot.
The position and orientation of the hand is determined by deflection of the
various joints of the robot arm. Suppose that there are n joints, each of which
bends in only one plane (this assumption is not essential). We then have to give
n numbers in order to specify the state of the joints. In the case n=2, we could
draw a diagram on a sheet of paper with one axis for each joint, so that a point
on the diagram would correspond to a possible state of the joints. If n>3, then
such a diagram would have to be n-dimensional, so we could not draw it.
Nevertheless, we can still reason about a theoretical n-dimensional space (call
it X) in which a single point represents a state of the arm. Now consider the
position and orientation of the hand. In the usual way, we need three
coordinates to specify the position. We next need to specify the direction in
which the central axis of the hand points. This needs two numbers: the angle of
elevation above the horizontal and the horizontal compass bearing. Note that
these two numbers are not entirely independent or well defined. If the elevation
is vertical then the compass bearing is meaningless. Also, the physical meaning
of the compass bearing is unchanged if we add 360 degrees. We can suppress this
by insisting that all angles must be taken between 0 and 360, but then we have a
different problem in that the numerical value of the angle could change suddenly
(as the arm moves from 1 degree to 359 degrees) without any genuine
discontinuity in the behaviour of the robot. There is a topological reason for
these problems. If the space of possible orientations of the hand could be
simply parametrised by two variables, then it would be topologically a plane.
However, it is not a plane. It can instead be thought of as the surface of a
sphere, which one imagines centered at a point on the axis of the hand. If the
hand held a torch, it would mark a point on the sphere which would determine the
orientation. There is one further variable to consider, viz. the twist of the
hand about its central axis. This gives a third angle, which again interacts in
a complicated way with the other two. All told, we need six parameters to
describe the position and orientation of the hand. We can thus consider a six
dimensional space Y, each point in which corresponds to a possible state of the
hand. We can analyse the structure of Y using the methods of algebraic topology,
and learn a number of interesting and nontrivial things about it. Each point in
our space X corresponds to a state of the joints of the robot. The state of the
joints determines the position and orientation of the hand. Thus, to each point
x in the space X we associate a point of Y, which we shall call f(x). However,
if we want to achieve a specified position and orientation of the hand, there
will in general be many ways to do this. In other words, many different points
of X will be associated to the same point of Y. It would be convenient in the
design and use of such robots to have a so-called ``inverse mapping''. For each
position and orientation of the hand (corresponding to a point y in Y) one would
like to choose a state of the joints (corresponding to a point g(y) of X) which
puts the hand in that situation (so that f(g(y))=y). Moreover, one would like
g(y) to vary continuously with y, so that similar positions of the hand are
achieved by similar states of the joints. It turns out, however, that this is
topologically impossible. It is thus necessary to devise a more complex control
strategy, in which the same hand position may be achieved in different ways at
different times. This is typical of the kind of information which can be
supplied by topological theory.
|

