Product Topology
The
topology
on the
Cartesian product
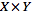of two
topological spaces whose open sets are the unions of subsets
 ,
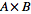where
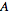and
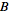are open subsets of
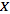and
 ,
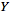respectively.
This definition extends in a natural way to the
Cartesian product of any finite number
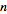of
topological spaces. The product topology of
where
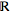is the real line with the
Euclidean topology, coincides with the
Euclidean topology of the
Euclidean space
 .
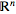In the definition of product topology of
 ,
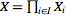where
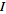is any set, the open sets are the unions of subsets
 ,
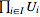where
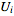is an open subset of
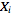with the additional condition that
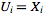for all but finitely many indices
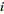(this is automatically fulfilled if
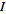is a finite set). The reason for this choice of open sets is that these are the
least needed to make the projection onto the
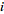 th
factor
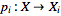continuous for all indices
 .
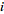Admitting all products of open sets would give rise to a larger topology
(strictly larger if
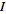is infinite), called the box topology.
The product topology is also called Tychonoff topology, but this
should not cause any confusion with the notion of
Tychonoff space, which has a completely different meaning.
|
