From Wikipedia, the free encyclopedia
Jump to:
navigation,
search
In
topology, Urysohn's lemma, sometimes called "the first
non-trivial fact of point set topology", is commonly used to
construct
continuous functions of various properties on
normal spaces. It is widely applicable since all
metric spaces and all
compact
Hausdorff spaces are normal. The lemma is generalized by (and
usually used in the proof of) the
Tietze extension theorem.
The lemma is named after
Pavel Samuilovich Urysohn. See also
Cutoff function.
Formal
statement
Urysohn's lemma states that X is a
normal
topological space if and only if, whenever A and B are
disjoint
closed
subsets of X, then there exists a
continuous function from X into the
unit interval [0, 1],
- f : X → [0, 1],
such that f(a) = 0 for all a in A and f(b)
= 1 for all b in B.
Any such function f is known as an Urysohn function.
Note that in the statement above, we do not, and in general cannot,
require that f(x) ≠ 0 and ≠ 1 for x outside of A
and B. This is only possible in
perfectly normal spaces.
A corollary of the lemma is that normal
T1
spaces are
Tychonoff.
Sketch
of proof
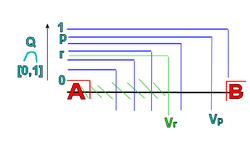
Illustration of Urysohn's "onion"
function.
For every
dyadic fraction r ∈ (0,1), we are going to construct an
open subset
U(r) of X such that:
- U(r) contains A and is disjoint from B
for all r
- for r < s, the
closure of U(r) is contained in U(s)
Once we have these sets, we define f(x) =
inf {
r : x ∈ U(r) } for every x ∈ X. Using
the fact that the dyadic rationals are
dense, it is then not too hard to show that f is continuous and
has the property f(A) ⊆ {0} and f(B) ⊆ {1}.
In order to construct the sets U(r), we actually do a
little bit more: we construct sets U(r) and V(r)
such that
- A ⊆ U(r) and B ⊆ V(r) for
all r
- U(r) and V(r) are open and disjoint for
all r
- for r < s, V(s) is contained in the
complement of U(r) and the complement of V(r)
is contained in U(s)
Since the complement of V(r) is closed and contains U(r),
the latter condition then implies condition (2) from above.
This construction proceeds by
mathematical induction. Since X is normal, we can find two
disjoint open sets U(1/2) and V(1/2) which contain A
and B, respectively. Now assume that n≥1 and the sets U(a/2n)
and V(a/2n) have already been constructed
for a = 1,...,2n-1. Since X is normal, we
can find two disjoint open sets which contain the complement of V(a/2n)
and the complement of U((a+1)/2n),
respectively. Call these two open sets U((2a+1)/2n+1)
and V((2a+1)/2n+1), and verify the above
three conditions.