Mechanism: the fundamental physical or chemical processes involved
in or responsible for an action, reaction or other natural phenomenon.
Machine: an assemblage of parts that transmit forces, motion and
energy in a predetermined manner.
Simple Machine: any of various elementary mechanisms having the
elements of which all machines are composed. Included in this category are the
lever, wheel and axle, pulley, inclined plane, wedge and the screw.
The word mechanism has many meanings. In
kinematics, a mechanism is a means of transmitting, controlling, or
constraining relative movement
(Hunt 78). Movements which are electrically, magnetically, pneumatically
operated are excluded from the concept of mechanism. The central theme for
mechanisms is rigid bodies connected together by joints.
A machine is a combination of rigid or resistant bodies, formed
and connected do that they move with definite relative motions and transmit
force from the source of power to the resistance to be overcome. A machine has
two functions: transmitting definite relative motion and transmitting force.
These functions require strength and rigidity to transmit the forces.
The term mechanism is applied to the combination of geometrical
bodies which constitute a machine or part of a machine. A mechanism
may therefore be defined as a combination of rigid or resistant bodies, formed
and connected so that they move with definite relative motions with respect to
one another
(Ham et al. 58).
Although a truly rigid body does not exist, many engineering
components are rigid because their deformations and distortions are negligible
in comparison with their relative movements.
The similarity between machines and mechanisms is that
- they are both combinations of rigid bodies
- the relative motion among the rigid bodies are definite.
The difference between machine and mechanism is that
machines transform energy to do work, while mechanisms so not necessarily
perform this function. The term machinery generally means machines
and mechanisms.
Figure 2-1 shows a picture of the main part of a diesel engine. The
mechanism of its cylinder-link-crank parts is a slider-crank mechanism,
as shown in
Figure 2-2.
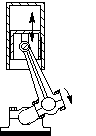Figure 2-1 Cross section of a power cylinder in a diesel engine
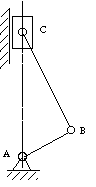Figure 2-2 Skeleton outline
Figure 2-3a shows an inclined plane, AB is the base, BC is the
height and AC the inclined plane. With the use of the inclined plane a
given resistance can be overcome with a smaller force than if the plane is not
used. For example, in
Figure 2-3b, suppose we wish to raise a weight of 1000 lb. through the
vertical distance BC = 2 ft. If this weight were raised vertically and without
the use of the inclined plane the force 1000 lb. would have to be exerted
through the distance BC. If, however, the inclined plane is used and the weight
is moved over its inclined plane AC, a force of only 2/3 of 1000 lb. or 667 lb.
is necessary, although this force is exerted through a distance AC which is
greater than distance BC.
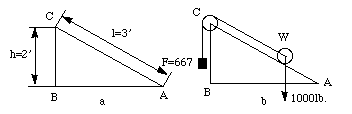
Figure 2-3 Inclined plane
Using an inclined plane requires a smaller force exerted through a
greater distance to do a certain amount of work.
Letting F represent the force required to raise a given weight on the
inclined plane, and W the weight to be raised, we have the proportion:
(2-1)
One of the most common application of the principle of the
inclined plane is in the screw jack which is used to
overcome a heavy pressure or raise a heavy weight of W by a much smaller
force F applied at the handle. R represents the length of the
handle and P the pitch of the screw, or the distance advances in
one complete turn.
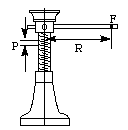
Figure 2-4 The screw jack
Neglecting the friction the following rule is used: The force F
multiplied by the distance through which it moves in one complete turn is equal
to the weight lifted times the distance through which it is lifted in the same
time. In one complete turn the end of the handle describes a circle of
circumference 2 R.
This is the distance through which the force F is exerted.
Therefore from the rule above
(2-2)
and
(2-3)
Suppose R equals 18 in., P equals 1/8 in. and the weight to be
lifted equals 100,000 lb., then the force required at F is then 110 lb.
This means that, neglecting friction, 110 lb. at F will raise 100,000 lb.
at W, but the weight lifted moves much slower than the force applied at
F.
A gear, or toothed wheel, when in operation, may actually be considered as a
lever with the additional feature that it can be rotated continuously, instead
of rocking back and forth through a short distance. One of the basic
relationships for a gear is the number of teeth, the diameter, and the rotary
velocity of gears.
Figure 2-5 shows the ends of two shafts A and B connected by 2 gears of 24
and 48 teeth respectively. Notice that the larger gear will make only one-half
turn while the smaller makes a complete turn. That is, the ratio of speeds
(velocity ratio) of the large to the smaller is as 1 to 2.
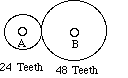
Figure 2-5 Gears
The gear that is closer to the source of power is called the driver,
and the gear that receives power from the driver is called the driven gear.
A gear train may have several drivers and several driven gears.
Figure 2-6 Gear train
When gear A turns once clockwise, gear B turns 4 times counter-clockwise and
gear C turns once clockwise. Hence gear B does not change the speed of C from
what it would have been if geared directly to gear A, but it changes its
direction from counterclockwise to clockwise.
The velocity ratio of the first and last gears in a train of simple gears
dose not changed by putting any number of gears between them.
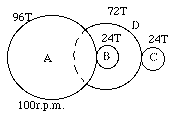
Figure 2-7 shows compound gears in which two gears are on the middle
shaft. Gears B and D rotate at the same speed since they are keyed (fixed) to
the same shaft. The number of teeth on each gear is given in the figure. Given
these numbers, if gear A rotates at 100 r.p.m. clockwise, gear B turns 400 r.p.m.
(rotations per minute) counterclockwise and gear C turns 1200 r.p.m. clockwise.
It is important when working with gears to know what number of teeth the
gears should have so that they can mesh properly in a gear train. The size of
the teeth for connecting gears must be match properly.
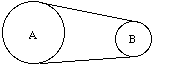
Belts and pulleys are an important part of most
machines. Pulleys are nothing but gears without teeth and instead
of running together directly they are made to drive one another by cords, ropes,
cables, or belting of some kinds.
As with gears, the velocities of pulleys are inversely proportional to their
diameters.
|
