|
A wheel provided with suitably shaped teeth, receiving an intermittent
circular motion from an oscillating or reciprocating member, is called a
ratchet wheel. A simple form of ratchet mechanism is shown in Figure 8-1.
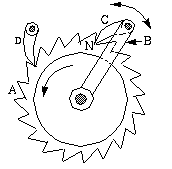
Figure 8-1 Ratchet
A is the ratchet wheel, and B is an oscillating lever
carrying the driving pawl, C. A supplementary pawl at D
prevents backward motion of the wheel.
When arm B moves counterclockwise, pawl C will force the wheel
through a fractional part of a revolution dependent upon the motion of B.
When the arm moves back (clockwise), pawl C will slide over the points of
the teeth while the wheel remains at rest because of fixed pawl D, and
will be ready to push the wheel on its forward (counterclockwise) motion as
before.
The amount of backward motion possible varies with the pitch of the teeth.
This motion could be reduced by using small teeth, and the expedient is
sometimes used by placing several pawls side by side on the same axis, the pawls
being of different lengths.
The contact surfaces of wheel and pawl should be inclined so that they will
not tend to disengage under pressure. This means that the common normal at N
should pass between the pawl and the ratchet-wheel centers. If this common
normal should pass outside these limits, the pawl would be forced out of contact
under load unless held by friction. In many ratchet mechanisms the pawl is held
against the wheel during motion by the action of a spring.
The usual form of the teeth of a ratchet wheel is that shown in the above
Figure, but in feed mechanisms such as used on many machine tools it is
necessary to modify the tooth shape for a reversible pawl so that the drive can
be in either direction. The following SimDesign example of a ratchet also
includes a four bar linkage.

If you try this mechanism, you may turn the
crank of the link mechanism. The
rocker will drive the
driving pawl to drive the
ratchet wheel. The corresponding SimDesign data file is:
/afs/andrew.cmu.edu/cit/ce/rapidproto/simdesign/ratchet.sim
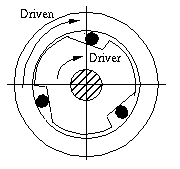
A special form of a
ratchet is the overrunning clutch. Have you ever thought about what
kind of mechanism drives the rear axle of bicycle? It is a free-wheel mechanism
which is an overrunning clutch. Figure 8-2 illustrates a simplified model. As
the driver delivers torque to the driven member, the rollers or balls are wedged
into the tapered recesses. This is what gives the positive drive. Should the
driven member attempt to drive the driver in the directions shown, the rollers
or balls become free and no torque is transmitted.
A pair of rotating members may be designed so that, for continuous rotation
of the driver, the follower will alternately roll with the driver and remain
stationary. This type of arrangement is know by the general term intermittent
gearing. This type of gearing occurs in some counting mechanisms,
motion-picture machines, feed mechanisms, as well as others.
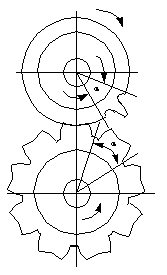
The simplest form of intermittent gearing, as illustrated in
Figure 8-3 has the same kind of teeth as ordinary gears designed for continuous
rotation. This example is a pair of 18-tooth gears modified to meet the
requirement that the follower advance one-ninth of a turn for each turn of the
driver. The interval of action is the two-pitch angle (indicated on both gears).
The single tooth on the driver engages with each space on the follower to
produce the required motion of a one-ninth turn of the follower. During the
remainder of a driver turn, the follower is locked against rotation in the
manner shown in the figure.
To vary the relative movements of the driver and follower,
the meshing teeth can be arranged in various ways to suit requirements. For
example, the driver may have more than one tooth, and the periods of rest of the
follower may be uniform or may vary considerably. Counting mechanisms are often
equipped with gearing of this type.
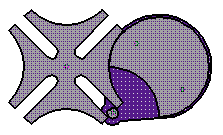
An interesting example of
intermittent gearing is the Geneva Wheel shown in Figure 8-4. In this
case the driven wheel, B, makes one fourth of a turn for one turn
of the driver, A, the pin, a, working in the
slots, b, causing the motion of B. The circular portion of the
driver, coming in contact with the corresponding hollow circular parts of the
driven wheel, retains it in position when the pin or tooth a is out of
action. The wheel A is cut away near the pin a as shown, to
provide clearance for wheel B in its motion.
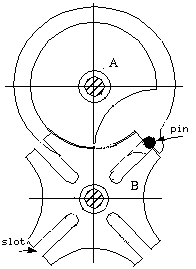
If one of the slots is closed, A can only move
through part of the revolution in either direction before pin a strikes
the closed slot and thus stops the motion. The device in this modified form was
used in watches, music boxes, etc., to prevent overwinding. From this
application it received the name Geneva stop. Arranged as a stop, wheel
A is secured to the spring shaft, and B turns on the axis of the
spring barrel. The number of slots or interval units in B depends upon
the desired number of turns for the spring shaft.
An example of this mechanism has been made in SimDesign,
as in the following picture.
The corresponding SimDesign data file is:
/afs/andrew.cmu.edu/cit/ce/rapidproto/simdesign/geneva.sim
The engine of an automobile is usually located in front part. How does it
connect to the rear axle of the automobile? In this case, universal joints are
used to transmit the motion.
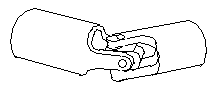
The universal joint as shown in Figure 8-5 is
also known in the older literature as Hooke's coupling. Regardless of how
it is constructed or proportioned, for practical use it has essentially the form
shown in Figure 8-6, consisting of two semicircular forks 2 and 4, pin-jointed
to a right -angle cross 3.
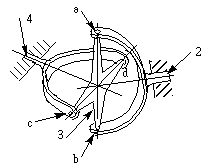
The driver 2 and the follower 4 make the complete
revolution at the same time, but the velocity ratio is not constant throughout
the revolution. The following analysis will show how complete information as to
the relative motions of driver and follower may be obtained for any phase of the
motion.
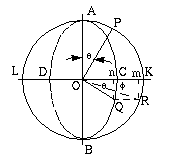
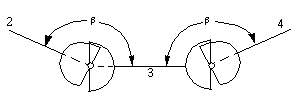
If the plane of projection is taken perpendicular to
the axis of 2, the path of a and b will be a circle AKBL as
shown in Figure 8-7.
If the angle between the shafts is
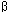 ,
the path of c and d will be a circle that is projected as the
ellipse ACBD, in which ,
the path of c and d will be a circle that is projected as the
ellipse ACBD, in which
OC = OD = OKcos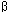 = OAcos
= OAcos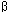 (8-1)
(8-1)
If one of the arms of the driver is at A, an
arm of the follower will be at C. If the driver arm moves through the
angle
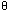 to P, the follower arm will move to Q. OQ will be
perpendicular to OP; hence: angle COQ =
to P, the follower arm will move to Q. OQ will be
perpendicular to OP; hence: angle COQ =
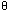 .
But angle COQ is the projection of the real angle describes by the
follower. Qn is the real component of the motion of the follower in a
direction parallel to AB, and line AB is the intersection of the
planes of the driver's and the follower's planes. The true angle .
But angle COQ is the projection of the real angle describes by the
follower. Qn is the real component of the motion of the follower in a
direction parallel to AB, and line AB is the intersection of the
planes of the driver's and the follower's planes. The true angle
 described by the follower, while the driver describes the angle
described by the follower, while the driver describes the angle
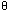 ,
can be found by revolving OQ about AB as an axis into the plane of the
circle AKBL. Then OR = the true length of OQ, and ROK
= ,
can be found by revolving OQ about AB as an axis into the plane of the
circle AKBL. Then OR = the true length of OQ, and ROK
=
 = the true angle that is projected as angle COQ =
= the true angle that is projected as angle COQ =
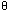 . .
Now
tan = Rm/Om
= Rm/Om
and
tan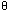 = Qn/On
= Qn/On
But
Qn = Rm
Hence
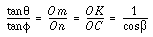
Therefore
tan = cos
= cos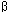 tan tan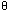
The ratio of the angular motion of the follower to
that of the driver is found as follower, by differentiating above equation,
remembering that
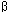 is constant
is constant
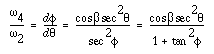
Eliminating
 : :
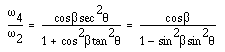
Similarly,
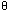 can be eliminated:
can be eliminated:
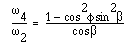
According to the above equations, when
the driver has a uniform angular velocity, the ratio of angular velocities
varies between extremes of cos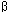 and 1/cos
and 1/cos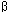 .
These variations in velocity give rise to inertia forces, torques, noise, and
vibration which would not be present if the velocity ratio were constant. .
These variations in velocity give rise to inertia forces, torques, noise, and
vibration which would not be present if the velocity ratio were constant.
By using a double joint shown on the right in
Figure 8-7, the variation of angular motion between driver and follower can
be entirely avoided. This compensating arrangement is to place an intermediate
shaft 3 between the driver and follower shafts. The two forks of this
intermediate shaft must lie in the same plane, and the angle between the first
shaft and the intermediate shaft must exactly be the same with that between the
intermediate shaft and the last shaft. If the first shaft rotates uniformly, the
angular motion of the intermediate shaft will vary according to the result
deduced above. This variation is exactly the same as if the last shaft rotated
uniformly, driving the intermediate shaft. Therefore, the variable motion
transmitted to the intermediate shaft by the uniform rotation of the first shaft
is exactly compensated for by the motion transmitted from the intermediate to
the last shaft, the uniform motion of either of these shafts will impart,
through the intermediate shaft, uniform motion to the other.
Universal joints, particularly in pairs, are used in many machines. One
common application is in the drive shaft which connects the engine of an
automobiles to the axle.
|

