|
Have you ever wondered what kind of mechanism causes the wind
shield wiper on the front widow of car to oscillate (
Figure 5-1a)? The mechanism, shown in
Figure 5-1b, transforms the rotary motion of the motor into
an oscillating motion of the windshield wiper.
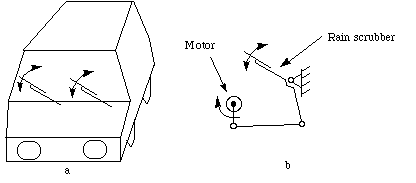
Figure 5-1 Windshield wiper
Let's make a simple mechanism with similar behavior. Take
some cardboard and make four strips as shown in
Figure 5-2a.
Take 4 pins and assemble them as shown in
Figure 5-2b.
Now, hold the 6in. strip so it can't move and turn the 3in.
strip. You will see that the 4in. strip oscillates.
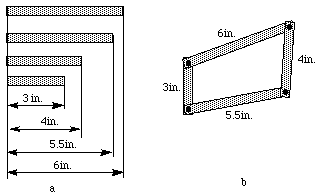
Figure 5-2 Do-it-yourself four bar linkage mechanism
The four bar linkage is the simplest and often times, the
most useful mechanism. As we mentioned before, a mechanism
composed of rigid bodies and lower pairs is called a
linkage
(Hunt 78). In planar mechanisms, there are only two kinds of
lower pairs ---
revolute pairs and
prismatic pairs.
The simplest closed-loop linkage is the four bar linkage
which has four members, three moving links, one fixed link and
four pin joints. A linkage that has at least one fixed link is a
mechanism. The following example of a four bar linkage was
created in
SimDesign in simdesign/fourbar.sim
Figure 5-3 Four bar linkage in SimDesign
This mechanism has three moving links. Two of the links are
pinned to the frame which is not shown in this picture. In
SimDesign, links can be nailed to the background thereby making
them into the
frame.
How many
DOF does this mechanism have? If we want it to have just
one, we can impose one constraint on the linkage and it will
have a definite motion. The four bar linkage is the simplest and
the most useful mechanism.
Reminder: A mechanism is composed of rigid bodies and lower
pairs called linkages
(Hunt 78). In planar mechanisms there are only two kinds of
lower pairs: turning pairs and prismatic pairs.
The function of a link mechanism is to produce rotating,
oscillating, or reciprocating motion from the rotation of a
crank or vice versa
(Ham et al. 58). Stated more specifically linkages
may be used to convert:
- Continuous rotation into continuous rotation, with a
constant or variable angular velocity ratio.
- Continuous rotation into oscillation or reciprocation
(or the reverse), with a constant or variable velocity
ratio.
- Oscillation into oscillation, or reciprocation into
reciprocation, with a constant or variable velocity ratio.
Linkages have many different functions, which can be
classified according on the primary goal of the mechanism:
- Function generation: the relative motion between
the links connected to the frame,
- Path generation: the path of a tracer point, or
- Motion generation: the motion of the coupler
link.
One of the simplest examples of a constrained linkage is the
four-link mechanism. A variety of useful
mechanisms can be formed from a four-link mechanism through
slight variations, such as changing the character of the pairs,
proportions of links, etc. Furthermore, many complex link
mechanisms are combinations of two or more such mechanisms. The
majority of four-link mechanisms fall into one of the following
two classes:
- the four-bar linkage mechanism, and
- the slider-crank mechanism.
Parallelogram Mechanism
In a parallelogram four-bar linkage, the orientation of the
coupler does not change during the motion. The figure
illustrates a loader. Obvioulsy the behavior of maintaining
parallelism is important in a loader. The bucket should not
rotate as it is raised and lowered. The corresponding SimDesign
file is simdesign/loader.sim.
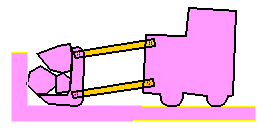
Figure 5-4 Front loader mechanism
Slider-Crank Mechanism
The four-bar mechanism has some special configurations
created by making one or more links infinite in length. The
slider-crank (or crank and slider) mechanism shown below is a
four-bar linkage with the slider replacing an infinitely long
output link. The corresponding SimDesign file is
simdesign/slider.crank.sim.
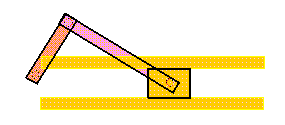
Figure 5-5 Crank and Slider Mechanism
This configuration translates a rotational motion into a
translational one. Most mechanisms are driven by motors, and
slider-cranks are often used to transform rotary motion into
linear motion.
Crank and Piston
You can also use the slider as the input link and the crank
as the output link. In this case, the mechanism transfers
translational motion into rotary motion. The pistons and crank
in an internal combustion engine are an example of this type of
mechanism. The corresponding SimDesign file is
simdesign/combustion.sim.
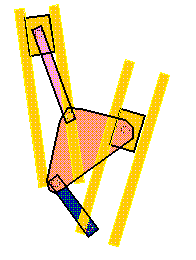
Figure 5-6 Crank and Piston
You might wonder why there is another slider and a link on
the left. This mechanism has two dead points. The slider and
link on the left help the mechanism to overcome these dead
points.
Block Feeder
One interesting application of slider-crank is the block
feeder. The SimDesign file can be found in
simdesign/block-feeder.sim
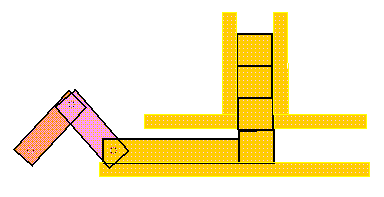
Figure 5-7 Block Feeder
In the range of planar mechanisms, the simplest group of
lower pair mechanisms are four bar linkages. A four bar
linkage comprises four bar-shaped links and four turning
pairs as shown in
Figure 5-8.
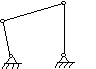
Figure 5-8 Four bar linkage
The link opposite the
frame is called the coupler link, and the links whick
are hinged to the frame are called side links. A link
which is free to rotate through 360 degree with respect to a
second link will be said to revolve relative to the
second link (not necessarily a frame). If it is possible for all
four bars to become simultaneously aligned, such a state is
called a change point.
Some important concepts in link mechanisms are:
- Crank: A side link which revolves relative to the
frame is called a crank.
- Rocker: Any link which does not revolve is called
a rocker.
- Crank-rocker mechanism: In a four bar linkage, if
the shorter side link revolves and the other one rocks (i.e.,
oscillates), it is called a crank-rocker mechanism.
- Double-crank mechanism: In a four bar linkage, if
both of the side links revolve, it is called a
double-crank mechanism.
- Double-rocker mechanism: In a four bar linkage,
if both of the side links rock, it is called a
double-rocker mechanism.
Before classifying four-bar linkages, we need to introduce
some basic nomenclature.
In a four-bar linkage, we refer to the line segment
between hinges on a given link as a bar where:
- s = length of shortest bar
- l = length of longest bar
- p, q = lengths of intermediate bar
Grashof's theorem states that a four-bar mechanism has
at least one revolving link if
s + l <= p + q
(5-1)
and all three mobile links will rock if
s + l > p + q
(5-2)
The inequality 5-1 is Grashof's criterion.
All four-bar mechanisms fall into one of the four categories
listed in Table 5-1:
Table 5-1 Classification of
Four-Bar Mechanisms
| Case |
l + s vers. p + q |
Shortest Bar |
Type |
| 1 |
< |
Frame |
Double-crank |
| 2 |
< |
Side |
Rocker-crank |
| 3 |
< |
Coupler |
Doubl rocker |
| 4 |
= |
Any |
Change point |
| 5 |
> |
Any |
Double-rocker |
From Table 5-1 we can see that for a mechanism to have a
crank, the sum of the length of its shortest and longest links
must be less than or equal to the sum of the length of the other
two links. However, this condition is necessary but not
sufficient. Mechanisms satisfying this condition fall into the
following three categories:
- When the shortest link is a side link,
the mechanism is a crank-rocker mechanism. The shortest link
is the crank in the mechanism.
- When the shortest link is the
frame of the mechanism, the mechanism is a double-crank
mechanism.
- When the shortest link is the coupler
link, the mechanism is a double-rocker mechanism.
In Figure 5-11, if AB is the
input link, the force applied to the output link, CD, is
transmitted through the coupler link BC. (That is,
pushing on the link CD imposes a force on the link AB,
which is transmitted through the link BC.) For
sufficiently slow motions (negligible inertia forces), the force
in the coupler link is pure tension or compression (negligible
bending action) and is directed along BC. For a given
force in the coupler link, the torque transmitted to the output
bar (about point D) is maximum when the angle
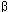between coupler bar BC and output bar CD is
 /2.
Therefore, angle BCD is called transmission angle.
(5-3)
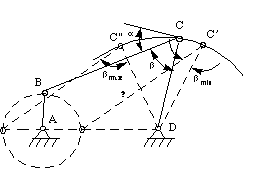
Figure 5-11 Transmission angle
When the transmission angle deviates significantly from
/2,
the torque on the output bar decreases and may not be sufficient
to overcome the friction in the system. For this reason, the
deviation angle
 =|/2-|
should not be too great. In practice, there is no definite upper
limit for
,
because the existence of the inertia forces may eliminate the
undesirable force relationships that is present under static
conditions. Nevertheless, the following criterion can be
followed.
When a side link such as AB in
Figure 5-10, becomes aligned with the
coupler link BC, it can only be
compressed or extended by the coupler. In this configuration, a
torque applied to the link on the other side, CD, cannot
induce rotation in link AB. This link is therefore said
to be at a dead point (sometimes called a toggle point).
Figure 5-10 Dead point
In Figure 5-11, if AB is a crank, it can become
aligned with BC in full extension along the line AB1C1
or in flexion with AB2 folded over B2C2.
We denote the angle ADC by
and the angle DAB by
 .
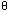We use the subscript 1 to denote the extended state and 2 to
denote the flexed state of links AB and BC. In the
extended state, link CD cannot rotate clockwise without
stretching or compressing the theoretically rigid line AC1.
Therefore, link CD cannot move into the forbidden zone
below C1D, and
must be at one of its two extreme positions; in other words,
link CD is at an extremum. A second extremum of link
CD occurs with
=
1.
Note that the extreme positions of a side link occur
simultaneously with the dead points of the opposite link.
In some cases, the dead point can be useful for tasks such as
work fixturing (Figure 5-11).
Figure 5-11 Work fixturing
In other cases, dead point should be and can be overcome with
the moment of inertia of links or with the asymmetrical
deployment of the mechanism (Figure 5-12).
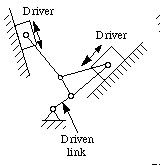
Figure 5-12 Overcoming the dead point by asymmetrical
deployment (V engine)
The slider-crank mechanism, which has a well-known
application in engines, is a special case of the
crank-rocker mechanism. Notice that if
rocker 3 in Figure 5-13a is very long, it
can be replaced by a block sliding in a curved slot or guide as
shown. If the length of the rocker is infinite, the guide and
block are no longer curved. Rather, they are apparently
straight, as shown in Figure 5-13b, and the
linkage takes the form of the ordinary slider-crank mechanism.
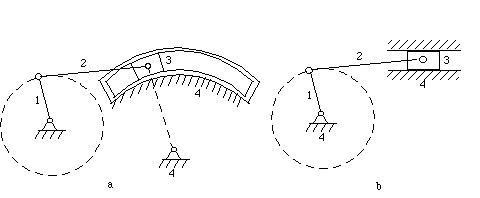
Figure 5-13 Slider-Crank mechanism
Inversion is a term used in kinematics for a reversal
or interchange of form or function as applied to
kinematic chains and mechanisms. For example, taking a
different link as the fixed link, the slider-crank mechanism
shown in Figure 5-14a can be inverted into
the mechanisms shown in Figure 5-14b, c, and d. Different
examples can be found in the application of these mechanisms.
For example, the mechanism of the pump device in
Figure 5-15 is the same as that in Figure
5-14b.
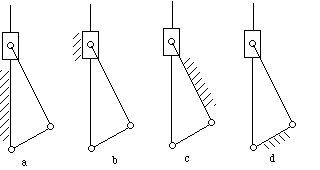
Figure 5-14 Inversions of the crank-slide mechanism
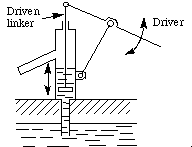
Figure 5-15 A pump device
Keep in mind that the inversion of a mechanism does not
change the motions of its links relative to each other but does
change their absolute motions.
|
