Statically equivalent force and moment systems
6.1 Definition of statically equivalent systems
of forces and moments
Two force systems that exert the same resultant force and resultant moment are
said to be statically equivalent (they have the same effect on the motion
of a rigid body).
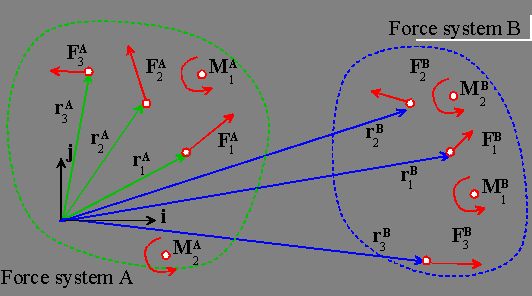
To make this precise, let force system A consist of forces
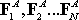
acting
at positions
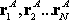 , ,
together with a set of moments
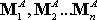
(we
don�t need to specify where the moments act).
Let force system B consist of forces
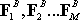
acting
at positions
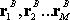 , ,
together with a set of moments
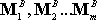
(we
don�t need to specify where the moments act).
The two force systems are statically equivalent if
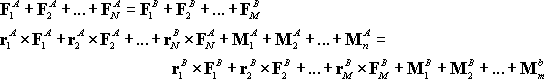
or in a rather more convenient shorthand notation
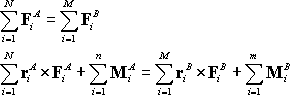
Note that
1.
Both force and moment sums must
be equal
2.
It doesn�t matter what point you
take moments about when testing for static equivalence, but you must take
moments about the same point for both force systems.
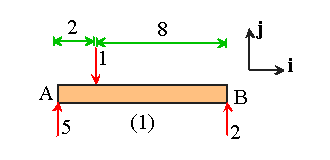
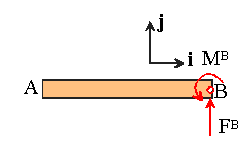
Here�s a simple problems to check that you understand the concept. The picture
below shows four different force systems acting on the same beam AB. All forces
are specified in N, distances in m, and moments in Nm. Find which force systems
are statically equivalent.
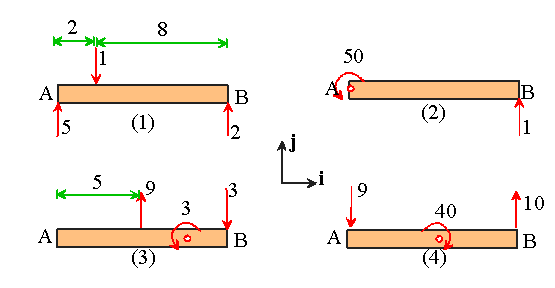
All we need to do is to calculate the resultant force and moment for each force
system (1)-(4). It�s easy to see that
1.
Force system 1: resultant force 6j ;
Resultant moment about A
18k
2.Force system 2: resultant force 1j ;
Resultant moment about A 60k
3.
Force system 3: resultant force 6j ;
Resultant moment about A
18k
4.
Force system 4: resultant force 1j ;
Resultant moment about A
60k
Therefore, force systems (1) and (3) are statically equivalent. Also, force
systems (2) and (4) are statically equivalent.
6.2 Replacing complex force and moment systems
with simpler statically equivalent systems
What�s the use of this definition? Well, we often find it convenient to
replace a complex force system with a simpler, statically equivalent system.
In the preceding section, we just checked to see whether a bunch of force
systems were statically equivalent. Usually, however, we are interested in
finding a simple force system (B, say) that replaces a complex force system
(A).
To this end, the following result is helpful
Any complex system of forces and moments is
statically equivalent to a single force acting at some specified position,
together with a moment.
To use this result, you need to choose where you want the equivalent force to
act. Then you can calculate the equivalent force and moment. The moment can
act wherever you like, but its magnitude and direction will depend on where you
choose to put the force.
In fact, we can find general formulas for the equivalent force and moment. Let
the complex force system A consist of forces
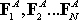
acting
at positions
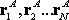 , ,
together with a set of moments
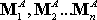 . .
Suppose we choose to replace force system A by a
single force
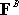
acting
at some convenient point
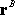 , ,
together with a moment
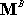 . .
Clearly the formula for
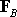 is
simply is
simply
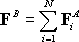
whereupon we find the following formula for
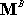
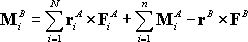
Let�s work through a few examples
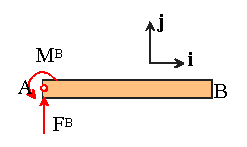
Example 1:
Replace the force system shown with a statically
equivalent force and moment acting (a) at point A; (b) acting at point B
It�s quicker to solve this problem by interpreting the meaning of the formulas
than by cranking through the vector algebra. The figure shows statically
equivalent forces and moments acting at A. We need to determine the unknown
force and moment.
The formulas say:
(1)
 is
equal to the resultant of the complex force system. Thus, is
equal to the resultant of the complex force system. Thus,
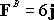
(2)
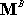 is
equal to the resultant moment of the complex force system, minus the moment of is
equal to the resultant moment of the complex force system, minus the moment of
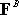 .
It doesn�t matter what point we take moments about to do this computation. For
the sake of variety, let�s take moments about B. The moment of the complex
force system about B is -42k. The moment of .
It doesn�t matter what point we take moments about to do this computation. For
the sake of variety, let�s take moments about B. The moment of the complex
force system about B is -42k. The moment of
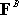 about
B is -60k. Therefore about
B is -60k. Therefore
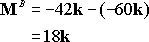
Now let�s repeat the exercise to get statically equivalent forces at B.
(1)
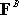 is
equal to the resultant of the complex force system. Thus, is
equal to the resultant of the complex force system. Thus,
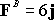
(2)
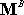 is
equal to the resultant moment of the complex force system, minus the moment of is
equal to the resultant moment of the complex force system, minus the moment of
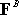 .
The moment of the complex force system about B is -42k. The moment of .
The moment of the complex force system about B is -42k. The moment of
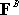 about
B is zero. Therefore about
B is zero. Therefore
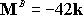 . .
Notice that the statically equivalent force is always the same,
regardless of where you put it. The moment depends on where you choose
to put the force, however.
Example 2:
In practice, statically equivalent force systems are used mostly to simplify
distributed loading. We�ve already seen that it�s a pain to calculate
resultant forces and moments of a distributed load. In any problem that
involves distributed loading, we usually start by replacing the distributed load
by a statically equivalent force and moment (or, as we shall see below, we can
sometimes replace the distributed load by a single force acting at a special
point).
For example, let�s replace the distributed force shown below by a statically
equivalent force and moment acting at A.
We�ve already calculated the resultant force and moment of the distributed
force. Remember that
(1)
The resultant force is
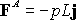
(2)
The resultant moment about A is
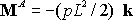
Therefore, the distributed force is statically equivalent to a force
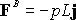 and
moment and
moment
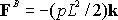 acting
at A, as shown below. acting
at A, as shown below.
If we needed to calculate reaction forces acting at A and B, for example, we
could now work with this simpler equivalent force system and forget about the
pressure.
6.3 An Application � Centers of Gravity for a
collection of solid objects
Sometimes it�s more convenient to try to replace a complex force system by a
single force, which is chosen to act at a special point, such that the moment
vanishes. Actually, this can�t always be done � it only works for
special force systems. Examples include
1.
Any 2D system of forces and moments
2.
Any set of parallel forces (eg gravity loading)
3.
Any pressure distribution acting normal to a surface.
4.
Any set of forces that act through a single point
It�s possible to derive a general formula for the force and its position, but
the derivation is a bit devious and the results aren�t particularly useful. If
you have a strong background in vectors and are up for a challenge you might try
to derive the result yourself � it�s a neat vector math problem. If you give up
the full scoop is here.
By far the most common situation where we need to work through this exercise is
to find the center of gravity of a collection of objects. In this case
we are actually replacing the forces of gravity (which act on each object) with
a statically equivalent force, exerting the same resultant force (the total
weight), and acting at a special point (the center of gravity) chosen to ensure
that the equivalent force also exerts the same resultant moment.
Most practical engineering
applications involve small objects close to the earth�s surface. In this case
the force of gravity can be taken to act in a fixed direction. Under these
conditions the center of gravity is the same as the center of mass.
There�s a simple formula for the position of the center of mass. Suppose we
have a collection of objects, with masses
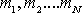 ,
centers of mass located at ,
centers of mass located at
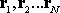 .
The position of the center of mass is for the
collection of objects is .
The position of the center of mass is for the
collection of objects is
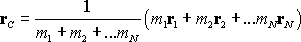
The same formula works with mass replaced by weight.
Example 1:
Calculate the position of the center of mass of
the object shown below, expressing your answer as coordinates relative to point
A in the basis shown. Evaluate the answer for the particular geometry h=a=b.
All parts have the same mass density.
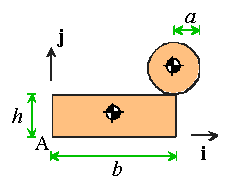
The center of gravity of each of the two parts is shown in the picture. It�s
convenient to do the calculation in a table. We will denote the mass per unit
area of each object by
The CG position follows by dividing the sum of the last column by the sum of the
second
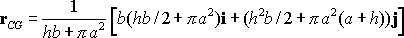
For the particular case when a=h=b we find
Example 2:
Calculate the position of the CG of a disk with a
hole in, shown below. Express your answer in terms of
 and and
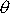 as
coordinates relative to the center of the disk. as
coordinates relative to the center of the disk.
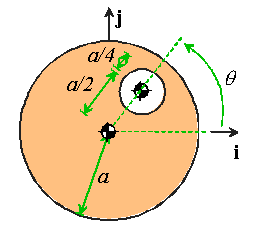
There�s a really neat trick for dealing with a hole � we can regard it as an
object with negative density!. So if the disk has mass density
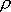 per
unit area, we treat the hole as an object with mass density per
unit area, we treat the hole as an object with mass density
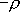 per
unit area, located at the position shown. per
unit area, located at the position shown.
So the CG position is
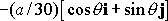
Example 3:
Aircraft weight and balance.
If you fly airplanes, you will regularly need to calculate the position of the
center of gravity for your aircraft. The center of gravity moves if you load
the plane with passengers, fuel and baggage. It�s very important to keep the
center of gravity within prescribed limits � if you don�t do so, the aircraft
may be unable to recover from a stall, or may even become uncontrollable.
FAA regulations require an accurate weight and balance record for each
aircraft, which is an official record of the planes empty weight, and the
position of its center of gravity when empty. The pilots operating handbook
specifies the positions of passenger seats, fuel containers and baggage
compartment. This information can be used to determine the position of the
center of gravity in any loaded configuration. The position can then be
compared with allowable limits.
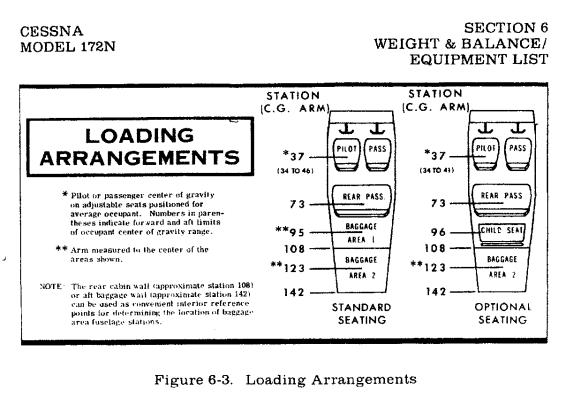
As an example, the picture below gives data for a Cessna Skyhawk C-172N. All
positions are reported as distances behind the firewall, in inches. THIS
INFORMATION IS NOT TO BE USED FOR ACTUAL FLIGHT PLANNING PURPOSES. ALWAYS
CONSULT THE POH FOR YOUR OWN AIRCRAFT.
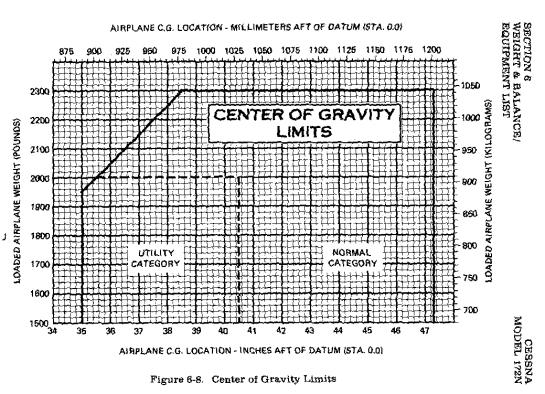
The operating manual also specifies admissible ranges for the position of the
CG. The data for a C-172N is shown below.
In addition to the data shown above, each aircraft has to be carefully weighed,
with all its equipment on board, but without fuel, oil, passengers and baggage,
to find the basic empty weight (BEW); and the basic empty CG arm.
Let�s suppose our airplane has a BEW of 1454lb, and a CG arm of 39.6 inches.
Suppose we plan a family trip with the following loading
1.
Pilot � 150lb
2.
Front seat passenger � 180lb
3.
Rear seat passengers 80lb+60lb
4.
Baggage 20lb
Basic empty weight (includes unusable fuel & oil) 1454lb
Fuel capacity � 43 gal, fuel tank CG arm 46 inches behind firewall datum
Fuel weight 6lb/gal
Is the CG within limits with full fuel? Will it remain within limits as fuel is
consumed?
We can use our formula to calculate the distance of the CG behind the firewall
For this calculation we only
need to work with one component of the position vector � the distance behind the
firewall
The CG position with full fuel follows as
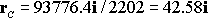
If all the fuel is used up the CG will move to
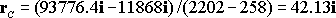
(FAA regulations require that you use at least a 30 min fuel reserve while
planning a daytime VFR flight; 45 mins for instrument flight or at night. The
laws of physics allow you to use all the fuel, but generally punish any attempt
to use more than the total fuel available rather severely)
We can check the position of the CG against the allowable range specified in the
operators manual. We are safely within limits both with full fuel and empty.
As fuel is used up, the CG moves along a straight line between the two end
points, so will remain within limits throughout the flight.
6.4 Simple problems involving replacing
distributed loads with statically equivalent forces
We showed in an earlier example how a distributed load, or pressure, can be
replaced by a statically equivalent force and moment. Often, it is preferable
to replace the distributed load using a statically equivalent force only,
which acts at a special point that is chosen so that the moment vanishes.
We�ve already seen the results of such calculations, in our discussion of
gravitational loading (distributed gravity load is replaced by a force acting at
the CG); hydrostatic loading (distributed fluid pressure is replaced by a
buoyancy force acting at the center of buoyancy) and drag and lift force
(distributed loading replaced by equivalent drag and lift forces acting at
center of lift).
So far, we don�t know how to actually calculate the location of the special
point (CG, center of buoyancy, etc).
In this section we show how to do this for simple 1-D distributed loads. Real
life is 3D, unfortunately, and you will learn how to solve 3D problems in later
courses.
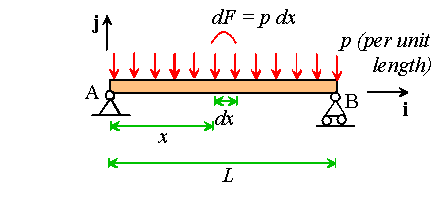
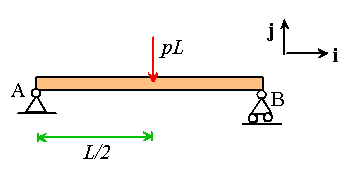
As a simple example, let�s
find the location of the statically equivalent force for a uniform pressure
acting on a beam. The beam has length L and is subjected to a
distributed load p per unit length. We�ll work with the coordinate
system shown in the picture.
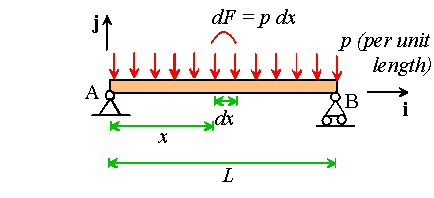
We already know that
(1)
The resultant force is
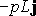
(2)
The resultant moment about A is
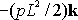
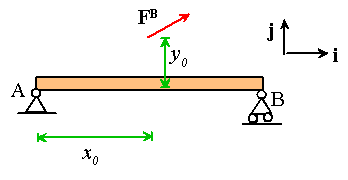
We now need to find a statically equivalent system, which consists of a single
force
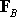 acting
at some special point acting
at some special point
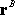 ,
chosen so that ,
chosen so that
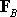 has
the same resultant force and moment. has
the same resultant force and moment.
For
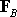 to
have the same resultant as the distributed load, we need to set to
have the same resultant as the distributed load, we need to set
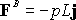
To find
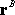 we
can set we
can set
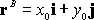 where where
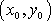 are
the unknown components of the position vector of are
the unknown components of the position vector of
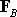 .
The moment of .
The moment of
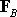 follows
as follows
as
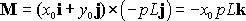
We need to make this moment equal to that of the distributed pressure, so that
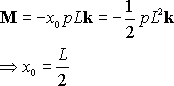
How about
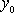 ?
We didn�t get an equation for it, so any value of ?
We didn�t get an equation for it, so any value of
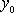 will
do. The reason for this, of course, is that you can always move the force will
do. The reason for this, of course, is that you can always move the force
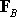 parallel
to itself without changing its resultant moment. Physically it makes sense to
think of the equivalent force as acting on the beam itself, so it makes sense to
choose parallel
to itself without changing its resultant moment. Physically it makes sense to
think of the equivalent force as acting on the beam itself, so it makes sense to
choose
 . .
The statically equivalent point force and its location are shown in the
picture.
|

