In Acoustics and Vibration, most periodic
waves, regardless of the form , can be represented by two or more sine waves.
Most waves can be reduced to simple harmonic or sine wave components which
generally form harmonic series. They have frequencies which are integral
multiples of the lowest frequency. The lowest frequency is called the
fundamental and the higher ones are called harmonic.
The Frequency of a vibrating body is the number of cycles
of motion in a unit time.
The Period of a wave is the time elapsed while the motion
repeats itself. It is the reciprocal of the frequency
The Amplitude of a wave is the shortest distance between
twp particles along the wave which differ in phase by one cycle.
The number of independent coordinates necessary to describe the
motion of a system is called the degrees of freedom. Examples of systems with
various degrees of freedom with a mass "M" are shown below.
Example (D) is a single degree of freedom with a mass "m"
supported on frictionless and mass-less rollers attached to a spring and a
dashpot.
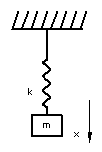
A) Single Degree of Freedom |
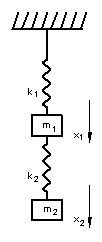
B) Two Degrees of Freedom |
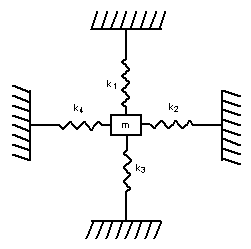
C) Multiple Degrees of Freedom |
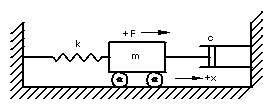
D) One Degree of Freedom
Linear Vibration |
| Where: |
| m |
= Mass of the system |
| c |
= Coefficient of viscous damping |
| k |
= Spring constant |
| x |
= Displacement from rest |
| F(t) |
= Displacement as a function of time |
|