Texture mapping

Texture Mapping

Texture mapping is a method for adding detail, surface texture, or colour to a computer-generated graphic or 3D model. Its application to 3D graphics was pioneered by Dr Edwin Catmull in his Ph.D. thesis of 1974.

Contents

• 1 Texture mapping
• 2 Perspective correctness
• 3 See also
• 4 References
• 5 External links

Texture mapping

A texture map is applied (mapped) to the surface of a shape, or polygon. This process is akin to applying patterned paper to a plain white box.

Multitexturing is the use of more than one texture at a time on a polygon. For instance, a light map texture may be used to light a surface as an alternative to recalculating that lighting every time the surface is rendered. Another multitexture technique is bump mapping, which allows a texture to directly control the facing direction of a surface for the purposes of its lighting calculations; it can give a very good appearance of a complex surface, such as tree bark or rough concrete, that takes on lighting detail in addition to the usual detailed coloring. Bump mapping has become popular in recent video games as graphics hardware has become powerful enough to accommodate it.

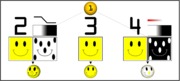
Examples of multitexturing
1. Untextured sphere 2. Texture and bump maps 3. Texture map only 4. Opacity and texture maps

The way the resulting pixels on the screen are calculated from the texels (texture pixels) is governed by texture filtering. The fastest method is to use the nearest-neighbour interpolation, but bilinear interpolation or trilinear interpolation between mipmaps are two commonly used alternatives which reduce aliasing or jaggies. In the event of a texture coordinate being outside the texture, it is either clamped or wrapped.

Perspective correctness

Because affine texture mapping does not take into account the depth information about a polygon's vertices, where the polygon is not perpendicular to the viewer it produces a noticeable defect.

Texture coordinates are specified at each vertex of a given triangle (for graphics hardware, polygons are generally broken down into triangles for rendering), and these coordinates are interpolated using an extended Bresenham's line algorithm. If these texture coordinates are linearly interpolated across the screen, the result is affine texture mapping. This is a fast calculation, but there can be a noticeable discontinuity between adjacent triangles when these triangles are at an angle to the plane of the screen (see figure at right).

Perspective correct texturing accounts for the vertices' positions in 3D space, rather than simply interpolating a 2D triangle. This achieves the correct visual effect, but it is slower to calculate. Instead of interpolating the texture coordinates directly, the coordinates are divided by their depth (relative to the viewer), and the reciprocal of the depth value is also interpolated and used to recover the perspective-correct coordinate. This correction makes it so that in parts of the polygon that are closer to the viewer the difference from pixel to pixel between texture coordinates is smaller (stretching the texture wider), and in parts that are farther away this difference is larger (compressing the texture).

Affine texture mapping directly interpolates a texture coordinate between two endpoints and :

where

Perspective correct mapping interpolates after dividing by depth , then uses its interpolated reciprocal to recover the correct coordinate:

Most modern graphics hardware implements perspective correct texturing, but when games still relied on software rendering, perspective correct texturing had to be used sparingly because of its computational expense. Several different techniques were developed to hide the defect of affine texture mapping. For instance, , Doom restricted the world to vertical walls and horizontal floors/ceilings. This meant the walls would be a constant distance along a vertical line and the floors/ceilings would be a constant distance along a horizontal line. A fast affine mapping could be used along those lines because it would be correct. A different approach was taken for Quake, which would calculate perspective correct coordinates only once every 16 pixels of a scanline and linearly interpolate between them, producing a compromise between the speed of affine texturing and perspective correctness.

Another technique was subdividing the polygons into smaller polygons and using an affine mapping on them. The distortion of affine mapping becomes much less noticeable on smaller polygons. Yet another technique was approximating the perspective with a faster calculation such as a polynomial. Finally, some programmers extended the constant distance trick used for Doom by finding the line of constant distance for arbitrary polygons and rendering along it.