VSEPR Theory

VSEPR Theory:

The Shapes of Molecules

One of the important ways that molecular compounds differ from ionic compounds is in their structures. Ionic bonding is nondirectional in the sense that, at a given distance, an ion will attract others of the opposite sign with the same force regardless of where these other ions are located around the ion in question - there is no preferred direction. Because of this, the way ions arrange themselves in an ionic solid is determined just by the tendency to maximize attractions between ions of opposite charge and to minimize repulsions between like-charged ions.

In molecular compounds, quite a different situation exists. Covalent bonds are highly directional. That is, for a given central atom in a molecule there are preferred orientations for the atoms attached to it, because covalent bonds are not formed with equal ease in all directions. As a result, in polyatomic molecules the atoms remain in the same relative orientation, regardless of whether the substance is a solid, liquid or a gas and we can say that the molecules have a definite structure or shape.

The shapes of molecules are very important because many of their physical and chemical properties depend upon the three-dimensional arrangements of their atoms. For example, the functioning of enzymes, which are substances that control how fast biochemical reactions occur, requires that there be a very precise fit between one molecule and another. Even slight alterations in molecular geometry can destroy this fit and deactivate the enzyme, which in turns prevents the biochemical reaction involved from occurring. Nerve poisons work this way.

There is a very simple theory that is remarkably effective in predicting the shapes of molecules formed by the representative elements. It is called the valence shell electron pair repulsion theory (VSEPR theory, for short). The theory is based on the idea that valence shell electron pairs, being negatively charged, stay as far part from each other as possible so that repulsions between them at a minimum.

Consider the BeCl₂ molecule. We've seen that its Lewis structure is

      ..       ..
    :Cl:Be:Cl:
     ..        ..
 

But how are these atoms arranged? Is BeCl₂ linear or is it nonlinear, that is, do the atoms lie in a straight line, or do they form some angels less than 180^o?

According to VSEPR theory, we can predict the shape of a molecule by looking at the electron pairs in the valence shell of the central atom. For BeCl₂, there are two pairs of electrons around the central beryllium atom. The question is, how can they locate themselves to be as far apart as possible? The answer is that the minimum repulsions will occur when the electron pairs are on opposite sides of the nucleus. (180^o apart).

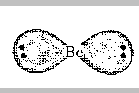
In order for the electrons to be in the Be-Cl bonds, the Cl atoms must be placed where the electrons are; the result is that we predict that a BeCl₂ molecule should be linear.

Cl-Be-Cl

Another example will be the BCl₃ molecule. Its Lewis structure is

        ..
      :Cl:
    ..  ..  ..
  :Cl:B:Cl:
    ..     ..

Here, the central atom, B, has three electron pairs. What arrangement will lead to minimum repulsions? The electron pairs will be as far apart as possible when they are located at the corners of a triangle with the boron in the centre.

When we attach the Cl atoms we obtain a triangular molecule.

This shape is planar triangular, because all four atoms lie in the equatorial plane.

In some molecules, all of the central pairs of the central atom are not bonding pairs. These unbonded pairs are actually unshared electron pairs - also called lone pairs - and these affect the geometry of the molecule. An example is SnCl₂.

     ..  ..   ..
   :Cl:Sn:Cl:
    ..        ..

There are three pairs of electrons around the central Sn atom - the two in the bonds plus the lone pair. As in BCl₃ , the mutual repulsions of the three pairs will place them at the corners of a triangle.

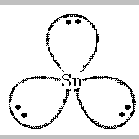
Adding on the two chlorine atoms gives

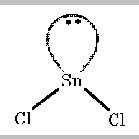
This is not a triangular shape, even though that is how the electron pairs are arranged. Molecular shape describes the arrangements of atoms, not the arrangement of electron pairs. Therefore, this shape is described as being bent.