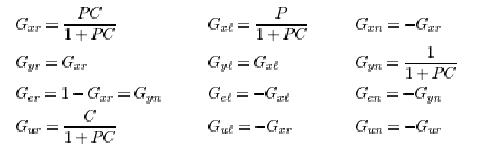
|
Here G.. denotes the transfer function from signal j to signal. Notice that there are only four independent transfer functions.
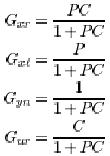
The transfer functions 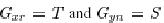 have special names, s is called the sensitivity function, and T is called the complementary sensitivity function. Notice that both S and T depend only on the loop transfer function L=PC. The sensitivity functions are related by
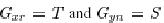
This explains the name complementary sensitivity function. These functions have interesting properties as is discussed in the following.
Stability and Stability Margins
Many properties of the system in figure 2 can be derived from the loop transfer function L=PC.
The stability of the system can be investigated by Nyquist�s stability criterion which says that the closed loop system is stable if
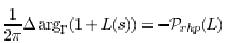
Where arg is the argument variation when traverses a contour that encloses the right half plane (RHP) and P (L) is the number of poles of L in the right half plane
Stability is normally investigated by analyzing the Nyquist curve, see Figure 3.
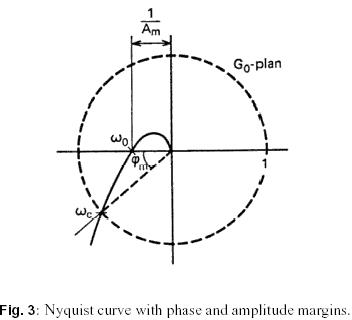
To achieve stability the Nyquist curve must be sufficiently far away from the critical point � 1. the
distance from the critical point can also be used as a measure of the degree of stability . in this
way
the notions of amplitude margin A and phase margin see figure 3. an amplitude margin A
implies
that the gain can be increased with a factor less than A without making the system
unstable.
Similarly for a system with a phase margin it is possible to increase the phase shift in the
loop by a quantity less than without making the system unstable.
1.1 Small Process Variations
The effects of small variations in the process will now be investigated. The signal transmission of the closed loop system from set point to output y is given by the complementary sensitivity function
Are also used as robustness measures. The variable 1/M can be interpreted as the shortest distance between the
Nyquist curve and the critical point -1, figure 3. Classically the maximum complementary sensitivity is denoted by M
|
