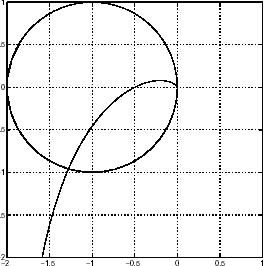
Fig. 4: Nyquist curve with circle for constant sensitivity S() =1.Disturbances with frequencies outside the circle are attenuated and frequencies inside the circle are amplified by the feedback.
1.2 A Property of the Sensitivity Function
The sensitivity function also has other physical interpretations. Consider the system in Figure 2. if there is no
feedback the lap lace transform of the output is Y.The output
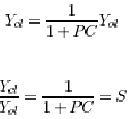
The sensitivity function thus tells how the disturbance are influenced by feedback. Disturbances with frequencies such that is less than one are reduced by an amount equal to the distance to the critical point and
disturbance with frequencies such that is larger larger than one are amplified by the feedback,. This illustrated in figure 4.
1.3 Large Process Variations
Equation 5 gives the sensitivity for small perturbations of the process. It is also possible to get expressions for large variations in the process. To see now much the process can change without making the closed
loop system unstable we will use the Nyquist curve in figure 4. the distance to the critical points is [1+L].if the changes by P the point changes by the system will remain stable as long as
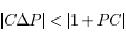
And the number of right hand poles of PC does not change. This implies that the perturbations must have the property that a P does not have any poles in the right half plane
The admissible variation is process dynamics is thus given by
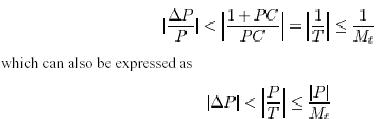
A crude estimate of the largest admissible variation in the process is thus given by the largest value M of the complementary sensitivity. It follows from the figure 4 that large variations in P are permitted for the frequencies where P either is large or small. the smallest admissible variations are for frequencies where | T |is large. A similar estimate based on the maximum sensitivity is that
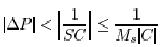
Bode�s Integrals
It follows from Equations and that it would be highly desirable to make the sensitivity functions S and T as
small as possible. This is unfortunately not possible because it follows from Equation (3) that S+T=1. there
are also other constraints on the sensitivities. It was show in [11] that
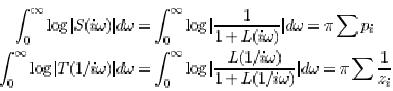
Where are the right half plane poles of L and are the right half plane zeros of L. These equations imply that the sensitivities can be made small at one frequency only at the expense of increasing the sensitivity at other frequencies. This phenomena is sometimes called the water bed effect. It also follows from the equations that the presences of poles in the right half plane increase the sensitivity and that zeros in the right half plane increase the complementary sensitivity. A fast RHP pole gives higher sensitivity than a slow pole, and a slow RHP zero gives higher sensitivity than a fast zero.
|