Controllability and observability

The fundamental controllability problem is associated with the question whether an input can be found such that the system states can be steered from an initial value Xo to any final value X1 in a given time interval. In general the answer to this question depends to this question depends on the time interval. This induces different notions of controllability ( uniform, instantaneous, differential) all of which become equivalent for linear time invariant systems. In the following discussion, only this simpler case is considered.

Proof: (if) since M is positive definite, it is nonsingular and therefore its inverse is well-defined. Define the input as Then by direct substitution, it follows that x(t1) = X1.(only if) this is a more involved argument and we will need the following intermediate result.

an elegant re-statement of the last property comes with the interpretation of controllability as a rank condition on the linear map that relates inputs to final states. That is consider the linear map.

It is now easy to verify that the adjoint map is a multiplier mapping vectors into functions:

Also recall that all solutions are now parameterized as where the null space is composed of functions orthogonal to the range of A. The controllability condition in terms of the Gramian is an extremely useful tool both for analysis and for numerical computations. Still, other equivalent conditions may be more convenient to check, depending on the problem at hand. Staying with the Gramian for the moment , a simple computation establishes the intuitive result if A,B) is c.c. in an interval [to,t1 ] it is also c.c. in any interval [to.t1] for any t2>t1.

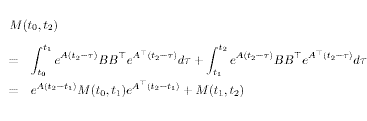
Since the last term is always positive semidefinite and the matrix exponential is always nonsingular, the desired result follows. Furthermore, for time invariant systems a simple change of variables under the integral shows that controllability is equivalent to the no singularity of M0,t). combining the two we get that.
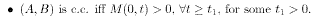