stability and Conversion

Through a different line of arguments, it can be shown that in the time invariant case controllability on an interval also implies controllability on a smaller interval. This last statement makes controllability easier to check for Hureitz Z since M(0,00) can be computed solving a simple lyapunov equation:

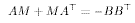
We have already seen that this computation produces a positive definite solution M when BBt>0. the same is true if (A,B) is controllable. When A is not Hurwitz, the statement is still valid for any finite interval. However, the Gramian does not converge as too and cannot be computed as the solution of a Lyapunov equation. In this case different techniques should be employed (e.g., splitting A into stable and anti-stable parts).

A different equivalent controllability condition is obtained through the use of wronskians and the following two technical Lemmas:

The second lemma is more useful to our case since the functions involved are polynomials and exponentials. Thus, evaluation the wronskian at t= 0 we obtain the following controllability condition.

This condition is one of the easiest to check given A,B and holds regardless of the stability properties of A. However, it is not always the most suitable. Other conditions are obtained via transformations of the above basic conditions; they are summarized in the following theorem

Given any ser T of numbers in C there exists a matrix K such that spectrum of A+BK is equal to T; note that A,B,K are real, T should be symmetric about the real line. (pole placement condition)

Analogous results can be obtained for the observability problem. The fundamental question is posed as follows: Given the system x=Ax, y=Cx with x(t0) =Xo and measurements y(t) in an interval[t0,t1] find Xo. If this is possible, Xo is said to be observable then (A,C) is completely observable (c.o.). in terms of operators in vector spaces, the map from initial conditions to the output is given by a multiplier:

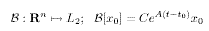
In general, this is a least squares problem; but in our noise-free case a solution exists and the main issue is the uniqueness of the solution. In other words, we seek to determine whether the operator B is 1-1. Its adjoint is an integral; operator

The observability Gramian is similar to the controllability Gramian with A,B being changed to � At,Ct. the remaining difference is in that M contains T1 while N contains t0. this can be fixed by pre-and post multiplying with eA(t0-t1) and its transpose. The latter being invertible does not change the rank properties of the matrix. This observation suggests a deeper duality between controllability and observability.

Thus, all our controllability conditions can be readily extended to the observability case. In particular, the observability matrix is now defined as

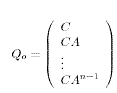
Instead of its transpose, and complete observability is equibalent to the invariability of QtQ. Furthermore whenever applicable, the infinite-interval Gramian is now found as the solution of the Lyapunov equation

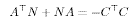
As a final remark, we should comment on the difference between the controllability Gramian and the controllability matrix. From the previous analysis they both provide necessary and sufficient conditions for controllability. The Gramian represents an integral condition while the matrix is associated with instantaneous (or, better, differential) properties. While equivalent for time � invariant systems, they produce different results with time-varying systems operator properties are concerned (optimal linear quadratic regulator, system reduction with a system gain criterion); the matrix appears in cases where the state-space representation is altered ( pole-placement control, conversion to canonical forms, structural versions of model reduction).