Optimal Linear Quadratic Regulators and Observers
Controllability and observability are central in the design of control systems since, among other properties, they guarantee the existence of a stabilizing controller. Such a controller can be designed as
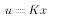
Where K is such that A+BK is Hurwitz( e.g., via the pole-placement equations). If the states of the system cannot be measured, them an observer based controller can achieve stabilization by setting u = - Kx where x is the state of an observer
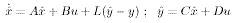Where K is such that A +LC is Hurwitz (e.g., via the dual to pole-placement equations). This observer-based controller satisfies the so-called separation principle, stating that the closed-loop eigenvalues are the eigenvalues of A+BK and the eigenvalues of A+LC. Even though stabilization is seemingly easy to achieve, the design of such a controller with desirable closed-loop properties (overshoot, bandwidth etc.) is more obscure.
In the 60�s the state-space approach became very popular with the application of optimal control theory. The optimal linear quadratic regulator (LQR) problem is defined as the design of a control input that minimizes an integral cost of the form
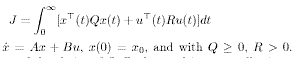
Subject to constraint an Important property of this design is that regardless of the choice of Q,R, the resulting controller is a stabilizing one. Moreover, it is always well-behaved and possesses some interesting and very desirable properties in terms of sensitivity peak magnitude. The separation principle was again invoked to design a controller by coupling the LQR with a Kalman Filter ( LQ- optimal observer). Unfortunately the result did not meet the expectations. The introduction of an observer in the loop can destroy the nice properties of the state-feedback LQR and introduce undesirable high gains in parts of the loop. This was manifested as a loss of robustness since a small amount of uncertainty could cause destabilization of the closed-loop.
Subsequently, the 80�s witnessed the rise of the H theory, which aimed to design controllers with optimal robustness properties. The classical notions of frequency comain peak magnitude, gain and phase margins came to the picture once again, though transformed to fit a multivariable framework. Here instead of the Q,R matrices the controller design parameters were multivariable transfer matrix weights. In the heart of the solution there was still an optimal LQ problem, except that now the controller and observer design equations were coupled. This is not surprising since the LQR possesses desirable induced-L2 gain. The results were then re-derived taking a differential game approach where a similar quadratic cost is minimized with the addition of an energy-bounded disturbance being the adversary.
In the following, we present some of the fundamental properties of the LQR theory. The basic LQR solution van be derived using Pontryagin�s minimum principle or the Bellman�s principle of optimality. The solution has the form
Where P is the positive definite solution of the so-called control algebraic Riccati equation (CARE)
Hence, V is at least negative semi-defite implying the stability of the zero equilibrium. If Q is only positive semi-definite then an additional argument is needed to establish asymptotic stability. This is known as laSalle�s tjeprem which states that the solution of the system differential equation that satisfies V = 0 is the trivial one. Hence, the states converge to zero asymptotically with time.
Another important result is related to the controller behavior in the presence of external disturbances and in particular input disturbances. Let us consider the system
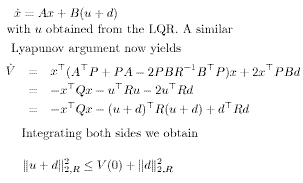
In other words, the gain of the closed-loop operator mapping d?u+d is less than one. In terms of classical control theory, this implies that closed-loop system has infinite gain margin and at least 60 deg. Phase margin for perturbations entering at the plant input. This type of result is central in the linear quadratic theory. One of its important by-products is that by augmenting the system with suitable weights, the operator from an external input to an output of interest can be manipulated to possess desirable properties (e.g., augmentation by an integrator)
Finally, the linear quadratic observer design can be performed as the dual of LQR. Here, L=PCtR-1 and P is the positive definite solution of the filtering ARE (FARE)
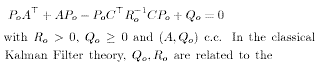
Output noise and state noise intensities (covariances). However, as previously mentioned, such a selection does not necessarily lead to good observer-based controllers. Instead, the H solution uses fictitious noise intensities, in addition to an augmentation with suitable filters, the closed-loop sensitivities in an optimal manner.
|
