Zero terminal-state MBPC
This can be regarded as the earliest and , conceptually, the simplest form of MBPC which guarantees stability to the controlled system, whenever feasibility is satisfied. Here ,Xn={0x} and , hence, the terminal-state constraint is the equality constraint
Given the plant state x, here Un(x), the set of feasible control sequences is the set of sequences which drive the plant initial state x to the zero-state in N steps with no constraint violation. Assume that Un(x) is non-empty, and satisfaction of all other conditions for the existence of the optimizing control sequence u(x) in(13). Then, asymptotic stability of the plant fed by the MBPC action can be easily proved by the following direct argument. Let U(x) be the control sequence obtained from U(x) by deleting its first control and inserting the zero-control 0u in its final position
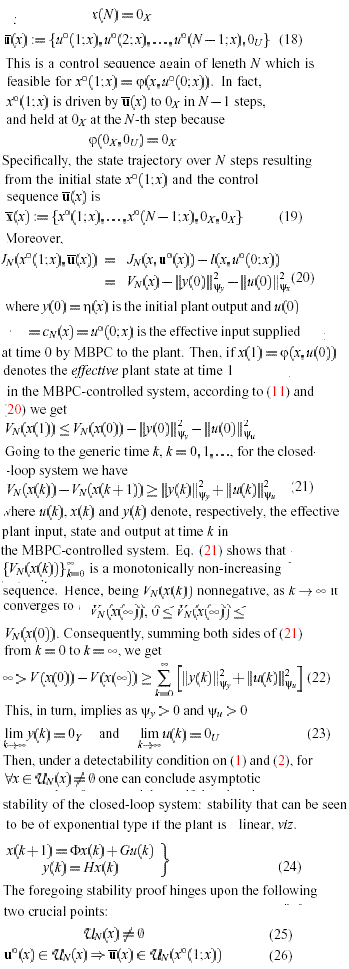
Now, feasibility condition (25) can be lost in zero terminal-state MBPC because of the need of driving the plant state to 0x in a finite time. If the initial state far from 0x, this brings about the use of large plants inputs which can violate possible input saturation constraints. Various approaches can be adopted so as to enlarge the set of admissible states (states such that (25) is fulfilled ). E. g., given a plant state x= 0x and an integer n1 such that un1(x)=0, one can always find, if the plant is controllable and make un2(x) non-empty. The disadvantages with this approach is that N2can be too large and , hence, the associated COLOC problem Pn1(x) too complex for an on-line solution for the available computing power and sampling time.
Hereafter, forms of MBPC will be presented which are particularly tailored for both solving the feasibility problem and yielding a highly performing closed-loop system. In so doing, for the sake of simplicity, we shall address linear plant of the form (22) in the presence of only input-saturation of constraints. The reason for the latter choice is that, while hard bounds on the manipulated variables are typically dictated by physical constraints, e, g. limited can be properly addressed by penalizing additional state-related constraints are frequently of the �soft-type�, and hence, can be properly addressed by penalizing additional state-related variables in the cost.
set-membership terminal constraint
Here, instead of using a terminal constraint consisting in an equality as (17), a set-membership terminal constraint x(N) E Xn is considered in the COLOC problem Pn(x). specifically ,we shall assume that the plant is linear in the from (24)with

|