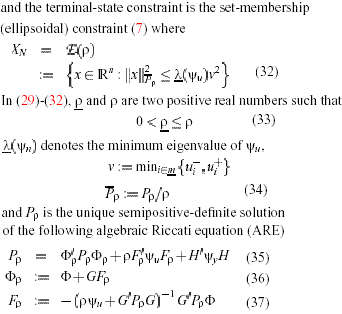
The x(Pp) denotes the maximum eigenvalue of fPp,. Further, for any initial state satisfying (39), the MBPC action satisfies the input saturation constraints at all times and makes the closed-loop system exponentially stable. The reader is referred to the appeasement for stability of the closed-loop system. The other interesting point is that the smaller Pp the larger the set of (admissible ) states satisfying (39). This is an important consideration in view of MBPC schemes where p-varying ellipsoidal constraints are adopted so as to maximize feasibility. One of such schemes is the subject of next section
Time-varying ellipsoidal terminal constraint
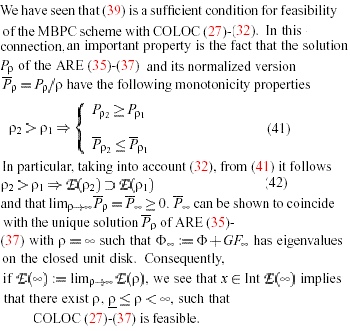
An important class of system consists of the linear time-invariant dynamical system whose states can be globally asymptotically steered to 0x by arbitrarily small controls. In the literature, these systems are referred to as ANCBI (asymptotically null controllable by bounded inputs) systems. A necessary and sufficient condition for a discrete-time time-invariant linear system be ANCBI is that it be stabilizable and have eigenvalues of modulus less than or equal to one, irrespective of thirmultiplicity. ANCBI system are very relevant to process control applications in that they encompass neutrally stable systems with chains of integrators of arbitrary complexity. Input-saturated ANCBI system are all and the only system for which it make sense to look for MBPC scheme with global feasibility and stability properties. Indeed, such schemes can be constructively devised on the grounds of (42) and the fact that for ANCBI systems.
Hence, for ANCBI system E(..)=IR. Therefore, for any ANCBI system, given an arbitrary xE IR� we can find p,p.less than p.. greater than under which COLOC (27)-(37) is feasible and the resulting closed-loop system exponentially stable. Now, for reason clarified in the next section which deals with step-wise disturbances, it is in practice important to handle unpredictable state jumps. Such jumps are responsible for the at a time t the plant state x(t) need not coincide with the one predicted in accordance with (24). Under such circumstances, in order to ensure feasibility, the p parameter in (27)-(37) has to be made state � dependent. In order to describe a possible answer to the problem, assume that at the event (x(t-1),t-1) the weight p was set equal to p(t-1), and COLOC (27)-(37) with p=p(t-1) generated the N (virtual) optimal controls
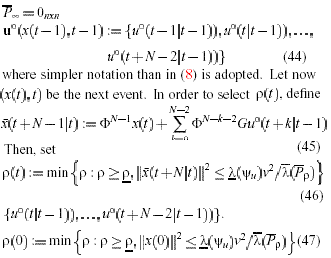
Here, x(t+N/t) can be seen to coincide with the state response at time t+N-1 from (x(t),t) to the input sequence Consequently p(t) as in (46) ensures that the mentioned control sequence drives x(t) .It follows that XOLOC (27)-(37)is savable at the current event (x(t),t) provided that that p is changed into the x(t)- dependent weight p(t) as in (46). The procedure can be initialized from the event (x(0),0) by taking (47)
|