Nonlinear Model Predictive Control

quasi-infinite horizon NMPC

IN the quasi-infinite horizon NMPC method [15.17]a terminal region constraint of the form (10) and a terminal penalty term as in (11) are added to the standard setup. As mentioned the terminal penalty term is not a performance specification that can be chosen freely. Rather E and the terminal region are determined off-line such that cost functional with terminal penalty term(11) gives an upper approximation of the infinite horizon cost functional with stage cost F thus closed-loop performance over the infinite horizon is addressed. Furthermore , as is shown later, stability is achieved , while only an optimization problem over a finite horizon must be solved. The resulting open-loop optimization problem is formulated as follows:

A formal proof of theorem I can be found in [14.16] and for a linear local controller as described below in [17] loosely speaking E is a local lyapunov function of the system under the local k(x) in as will be shown equation (15) allows to upper bound the optimal infinite horizon cost inside by the cost resulting from a local feedbox K(x)
Notice that the result in theorem 1 is nonlocal in nature, I, e their exists a region of attraction of at least the size of .the region of attraction is given by all states for which the open-loop optimal control problem has a feasible solution.
Obtaining a terminal penalty term E and a terminal region that satisfy the conditions of theorem 1 is not easy . if the linearized system is stabilizable and the cost function is quadratic with weight matrices Q and R, a locally linear feedback law u= kx can be used and the terminal penalty term can be approximated as quadratic of the form E(x)=xT px for this case a procedure to systematically compute the terminal region and a terminal penalty matrix off-line is available [17]. Assuming that the jacobian linearization(A,B) of (1) is stabilizable.

This procedure allows to calculate E and if the linearization of the system at the origin is stabilizable. If the terminal penalty term and the terminal region are determined according to theorem 1 the open-loop optimal trajectories found at each time instant approximate the optimal solution for the infinite horizon problem. The following reasoning make plausible: consider an infinite horizon cost functional defined by

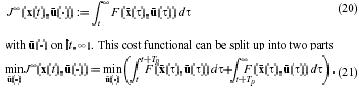
The goal is to upper approximate the second term by a terminal penalty term without further restrictions, this is not possible for general nonlinear system however if we ensure that the trajectories of the closed-loop system remain within some neighborhood of the origin (terminal region)for the time interval then an upper bound On the second term can be found. One possibility is to determine the terminal region such that a local state feedback law u=k(x) asymptotically stabilizes the nonlinear system and renders positiveliy omvariant for the closed-loop if an additional terminal inequality constraint (see(14d)) is added to problem, 1 then the second term of equation (21) can be upper bounded by the cost resulting from the application of this local controller u=k(x). note that the predicted state will not leave after t+Tp since u=k(x) renders positively invariant . Furthermore the feasibility at the next sampling instance is guaranteed dismissing the first part of u and replacing it by the nominal open-loop input resulting from the local controller. Requiring that and using the local controller for we obtain:

This implies that the optimal value of the finite horizon problem bounds that of the corresponding infinite horizon problem thus the prediction horizon can be thought of as extending quasi to infinity which given this approach its name, equation (24) can be exploited to prove theorem l.
Like in the dual-mode approach [56]. The use of the terminal inequality constraint gives the quasi-infinite horizon Nonlinear MPC scheme computational advantages, note also that as for as for dual-mode NMPC it is not necessary to find optimal solutions of problem l in order to guarantee stability, feasibility also implies stability here [17,70]. In difference to the dual-mode control however the local control law u=K(x) is never applied it is only used to compute the terminal penalty term E and the terminal region .
Many generalization and expansions of QIH-NMPC example discrete time variants can be determined such that (23) is exactly satisfied with equality [14], I, e. the horizon is recovered exactly , in [18,19,44] robust NMPC schemes using a min- max formulation are proposed, while in [27]an extension to index one DAE system is considered . a variation of QIH-NMPC for the control of the control of varying is given [28,30]