Nonlinear Model Predictive Control

Differ, there is no guarantee that the closed-loop system will be . it is indeed easy to construct examples for which the closed-loop becomes unstable if a (small) finite horizon is chosen. Hence when using finite horizons in standard NMPC,the stage cost cannot be chosen simply based on the desired physical objectives The overall basic structure of a NMPC control loop is depicted in figure 3 . as can be seen, it is necessary to estimate

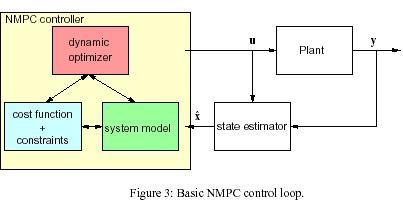
The system states from the output measurements. Summarizing the basic NMPC scheme works as follows:
1. obtain measurements/estimates of the states of the system
2. compute an optimal input signal by minimizing a given cost function over a certain prediction horizon in the future using a model of the system
3. implement the first part of the optimal input signal unit new measurements/estimates of the state are available
4. continue with 1.
From the remarks given so far and from the basic NMPC setup one can extract the following key characteristics of NMPC:
� NMPCallows the use of a nonlinear model of predictive.
� NMPC allows the explicit consideration of state and input constrains.
� In NMPC a specified performance criteria is minimized on-line.
� In NMPC the predicted behavior is in general different from the closed loop behavior.
� The on-line solution of an open �loop optimal control problem is necessary for the application of NMPC.
� To perform the prediction the system states must be measured or estimated. In the remaining section various aspects of NMPC regarding these properties will be discussed. The next section focuses on system theoretical aspects of NMPC. Especially the question on closed-loop stability robustness and the output feedback problem are considered.

System Theoretical Aspects of NMPC

In this different system theoretical aspects of NMPC are considered besides the question of nominal of stability of the closed-loop which can be considered as somehow mature today. Remarks on robust NMPC strategies as well as the output-feedback are given.

stability

One of the key in NMPC is certainly, whether a finite horizon NMPC strategy does lead to stability of the closed-loop. As pointed out the key problem with a finite prediction and control horizon stems from the fact that the predicted open and the resulting closed-loop behavior is in general different. Ideally one would seek for a NMPC strategy that achieves closed-loop stability independent of the choice of the performance parameters in the cost functional and, if possible, approximates the infinite horizon NMPC scheme as possible. A NMPC strategy that achieves closed-loop stability independent of the choice of the performance parameters is usually referred to a NMPC approach with guaranteed stability . different possibilities to achieve closed-loop stability for NMPC using finite horizon length nave been proposed. After giving a short review about these approaches we exemplary present on specific approach that achieves guaranteed stability, the so called quasi-infinite horizon approach to NMPC(QIHNMPC). This approach achieves guaranteed closed loop stability while being computationally feasible.
Here only the key ideas are reviewed and no detailed proofs are given, furthermore notice, that we not cover all existing NMPC approaches, instead we refer the reader to the overview papers[4.22.52.] For all the following section it is assumed that the prediction horizon is set equal to the control horizon Tp=Tc

infinite horizon NMPC

The most intuitive way to achieve stability is the use of an infinite horizon cost[10.39.54],i.e..Tp in problem 1 is set to . in the nominal case follows from bellman�s principle of optimality [7]., i.e the input and state trajectories computed as the solution of the NMPC optimization problem 1 at a specific instance in time, are in fact equal to the closed-loop trajectories of the nonlinear system ,I e. the remaining parts of the trajectories after one sampling instance are the optimal solution at the next sampling instance. This fact slso implies closed-loop stability.

Key ideas of the stability proof: since nearly all stability proofs for NMPC follow along the same basic steps as for the infinite horizon proof, the key ideas are shortly outlined. In principle the is based on the use of the value function as a lyapunov function. First it is shown that feasibility at one sampling instance does imply feasibility at the next sampling instance for the nominal case. In a second step it is established that the value function is strictly decreasing and by this the state and input converge to the origin utilizing the continuity of the value function the origin and the monotonicity property, asymptotic stability , the set of all states, for which the open-loop optimal control problem has a solution does belong to the region of attraction of the origin.

finite Horizon NMPC Schemes with guaranteed stability

Different possibility to achieve closed-loop stability for NMPC using a finite horizon length have been proposed, see for example [3,17,20,23,34,35,38,39,44,51,56,60,62,63,70]. Most of these approaches modify the NMPC setup such that stability of the closed-loop can be guaranteed independently of the plant and performance specifications. This is usually achieved by adding suitable equality or inequality constraints and suitable additional penalty terms to the cost functional. These additional constraints are usually not motivated by physical restrictions or desired performance requirements but have the sle purpose to enforce stability of the closed-loop. Therefore, they are usually termed the simplest possibility to enforce stability with a finite prediction horizon is to add a so called

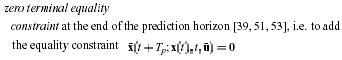
To problem 1. this leads to stability of the closed-loop if the optimal control problem possesses a solution at t=o, since the feasibility at one time instance does also leads to feasibility at the following time instances and a decrease in the value function. One disadvantage of a zero terminal constraint is that the system must be brought to the origin in finite time, this leads in general to feasibility problems for short prediction/control horizon lengths, i.e. a small region of attraction additionally from a computational point of view an exact satisfaction of a zero terminal equality constraint does require an infinite number of iterations in the nonlinear programming problem[17]. On the other hand, the main advantages are the straightforward application and conceptual simplicity.

Many schemes have been proposed (i.e [17,20,34,38,51,56,60,63]),that try to overcome the use of a zero terminal constraint of the form (9). Most of them either use a so called terminal region constraint

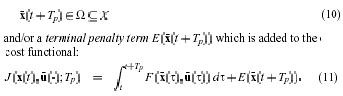
Note that the terminal penalty term is not a performance specification that can be chosen freely. Rather E and the terminal region in (10) are determined off �line such that stability is � enforced� . we not review all these methods here instead we exemplify the basic idea considering one specific approach, the so called quasi-infinite horizon NMPC approach [17]