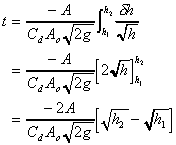
- Submerged Orifice
We have two tanks next to each other (or one tank separated by a dividing
wall) and fluid is to flow between them through a submerged orifice. Although
difficult to see, careful measurement of the flow indicates that the submerged
jet flow behaves in a similar way to the jet in air in that it forms a vena
contracta below the surface. To determine the velocity at the jet we first use
the Bernoulli equation to give us the ideal velocity. Applying Bernoulli from
point 1 on the surface of the deeper tank to point 2 at the centre of the
orifice, gives
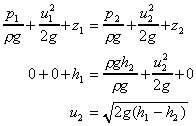
i.e. the ideal velocity of the jet through the submerged orifice depends on
the difference in head across the orifice. And the discharge is given by
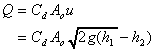
6. Time for Equalisation
of Levels in Two Tanks
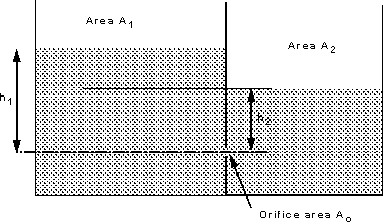
Two tanks of initially different levels joined by an orifice
By a similar analysis used to find the time for a level drop in a tank we can
derive an expression for the change in levels when there is flow between two
connected tanks.
Applying the continuity equation

Also we can write
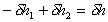
So
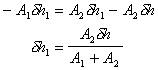
Then we get
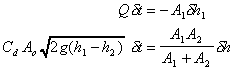
Re arranging and integrating between the two levels we get
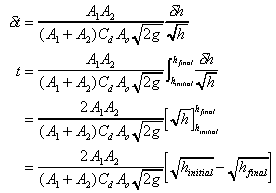
(remember that h in this expression is the difference in height
between the two levels (h2 - h1) to get the time
for the levels to equal use hinitial = h1 and hfinal
= 0).
Thus we have an expression giving the time it will take for the two levels to
equal.
Flow Over Notches and
Weirs
A notch is an opening in the side of a tank or reservoir which extends above
the surface of the liquid. It is usually a device for measuring discharge. A
weir is a notch on a larger scale - usually found in rivers. It may be sharp
crested but also may have a substantial width in the direction of flow - it is
used as both a flow measuring device and a device to raise water levels.
7. Weir Assumptions
We will assume that the velocity of the fluid approaching the weir is small
so that kinetic energy can be neglected. We will also assume that the velocity
through any elemental strip depends only on the depth below the free surface.
These are acceptable assumptions for tanks with notches or reservoirs with
weirs, but for flows where the velocity approaching the weir is substantial the
kinetic energy must be taken into account (e.g. a fast moving river).
8. A General Weir Equation
To determine an expression for the theoretical flow through a notch we will
consider a horizontal strip of width b and depth h below the free
surface, as shown in the figure below.

Elemental strip of flow through a notch

integrating from the free surface,
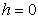 , to
the weir crest, , to
the weir crest,
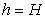 gives
the expression for the total theoretical discharge gives
the expression for the total theoretical discharge

This will be different for every differently shaped weir or notch. To make
further use of this equation we need an expression relating the width of flow
across the weir to the depth below the free surface.
9. Rectangular Weir
For a rectangular weir the width does not change with depth so there is no
relationship between b and depth h. We have the equation,

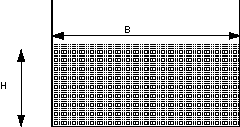
A rectangular weir
Substituting this into the general weir equation gives
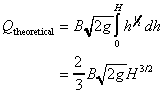
To calculate the actual discharge we introduce a coefficient of discharge,
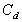 ,
which accounts for losses at the edges of the weir and contractions in the area
of flow, giving ,
which accounts for losses at the edges of the weir and contractions in the area
of flow, giving
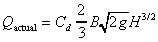
10. 'V' Notch Weir
For the "V" notch weir the relationship between width and depth is dependent
on the angle of the "V".
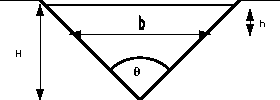
"V" notch, or triangular, weir geometry.
If the angle of the "V" is
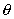 then
the width, b, a depth h from the free surface is then
the width, b, a depth h from the free surface is

So the discharge is
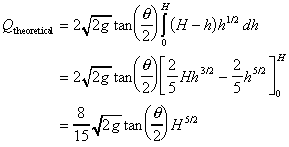
And again, the actual discharge is obtained by introducing a coefficient of
discharge

|

