The Bernoulli equation
1. Work and energy
We know that if we drop a ball it accelerates downward with an acceleration
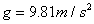 (neglecting the frictional resistance due to air). We can calculate the speed of
the ball after falling a distance h by the formula
(neglecting the frictional resistance due to air). We can calculate the speed of
the ball after falling a distance h by the formula
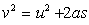 (a
= g and s = h). The equation could be applied to a falling droplet of
water as the same laws of motion apply (a
= g and s = h). The equation could be applied to a falling droplet of
water as the same laws of motion apply
A more general approach to obtaining the parameters of motion (of both solids
and fluids) is to apply the principle of conservation of energy.
When friction is negligible the
sum of kinetic energy and gravitational potential energy is constant.
Kinetic energy
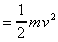
Gravitational potential energy
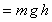
(m is the mass, v is the velocity and h is the height
above the datum).
To apply this to a falling droplet we have an initial velocity of zero, and
it falls through a height of h.
Initial kinetic energy
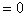
Initial potential energy
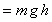
Final kinetic energy
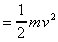
Final potential energy
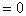
We know that
kinetic energy + potential energy = constant
so
Initial kinetic energy + Initial potential energy = Final kinetic energy +
Final potential energy
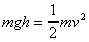
so
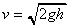
Although this is applied to a drop of liquid, a similar method can be applied
to a continuous jet of liquid.
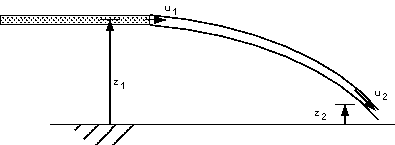
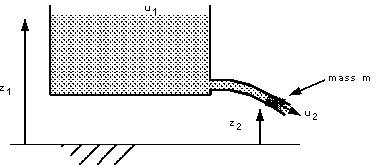
The Trajectory of a jet of water
We can consider the situation as in the figure above - a continuous jet of
water coming from a pipe with velocity
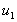 . One
particle of the liquid with mass . One
particle of the liquid with mass
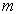 travels with the jet and falls from height
travels with the jet and falls from height
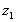 to to
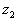 . The
velocity also changes from . The
velocity also changes from
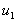 to to
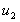 . The
jet is travelling in air where the pressure is everywhere atmospheric so there
is no force due to pressure acting on the fluid. The only force which is acting
is that due to gravity. The sum of the kinetic and potential energies remains
constant (as we neglect energy losses due to friction) so . The
jet is travelling in air where the pressure is everywhere atmospheric so there
is no force due to pressure acting on the fluid. The only force which is acting
is that due to gravity. The sum of the kinetic and potential energies remains
constant (as we neglect energy losses due to friction) so
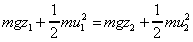
As 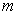 is
constant this becomes is
constant this becomes
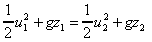
This will give a reasonably accurate result as long as the weight of the jet
is large compared to the frictional forces. It is only applicable while the jet
is whole - before it breaks up into droplets.
Flow from a reservoir
We can use a very similar application of the energy conservation concept to
determine the velocity of flow along a pipe from a reservoir. Consider the
'idealised reservoir' in the figure below.
An idealised reservoir
The level of the water in the reservoir is
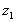 .
Considering the energy situation - there is no movement of water so kinetic
energy is zero but the gravitational potential energy is .
Considering the energy situation - there is no movement of water so kinetic
energy is zero but the gravitational potential energy is
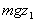 . .
If a pipe is attached at the bottom water flows along this pipe out of the
tank to a level
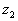 . A
mass . A
mass 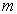 has flowed from the top of the reservoir to the nozzle and it has gained a
velocity
has flowed from the top of the reservoir to the nozzle and it has gained a
velocity
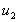 . The
kinetic energy is now . The
kinetic energy is now
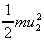 and
the potential energy and
the potential energy
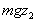 .
Summarising .
Summarising
Initial kinetic energy
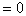
Initial potential energy
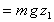
Final kinetic energy
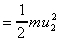
Final potential energy
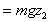
We know that
kinetic energy + potential energy = constant
so
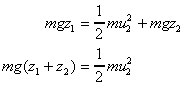
so
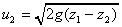
We now have a expression for the velocity of the water as it flows from of a
pipe nozzle at a height
 below
the surface of the reservoir. (Neglecting friction losses in the pipe and the
nozzle). below
the surface of the reservoir. (Neglecting friction losses in the pipe and the
nozzle).
Now apply this to this example: A reservoir of water has the surface at 310m
above the outlet nozzle of a pipe with diameter 15mm. What is the a) velocity,
b) the discharge out of the nozzle and c) mass flow rate. (Neglect all friction
in the nozzle and the pipe).
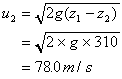
Volume flow rate is equal to the area of the nozzle multiplied by the
velocity
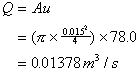
The density of water is
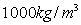 so
the mass flow rate is so
the mass flow rate is
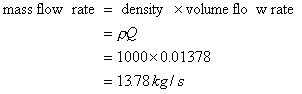
In the above examples the resultant pressure force was always zero as the
pressure surrounding the fluid was the everywhere the same - atmospheric. If the
pressures had been different there would have been an extra force acting and we
would have to take into account the work done by this force when calculating the
final velocity.
We have already seen in the hydrostatics section an example of pressure
difference where the velocities are zero.
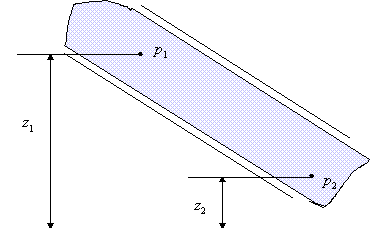
The pipe is filled with stationary fluid of density
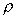 has
pressures has
pressures
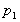 and and
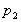 at
levels at
levels 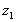 and
and 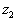 respectively. What is the pressure difference in terms of these levels?
respectively. What is the pressure difference in terms of these levels?
|

