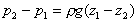
or
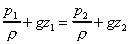
This applies when the pressure varies but the fluid is stationary.
Compare this to the equation derived for a moving fluid but constant
pressure:
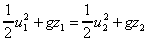
You can see that these are similar form. What would happen if both pressure
and velocity varies?
2. Bernoulli's Equation
Bernoulli's equation is one of the most important/useful equations in fluid
mechanics. It may be written,
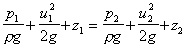
We see that from applying equal pressure or zero velocities we get the two
equations from the section above. They are both just special cases of
Bernoulli's equation.
Bernoulli's equation has some restrictions in its applicability, they are:
- Density is constant (which also means the fluid is incompressible);
- Friction losses are negligible.
- The equation relates the states at two points along a single streamline,
(not conditions on two different streamlines).
All these conditions are impossible to satisfy at any instant in time!
Fortunately for many real situations where the conditions are approximately
satisfied, the equation gives very good results.
The derivation of Bernoulli's Equation:
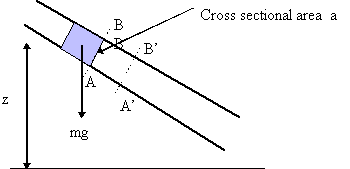
An element of fluid, as that in the figure above, has potential energy due to
its height z above a datum and kinetic energy due to its velocity u. If
the element has weight mg then
potential energy =
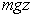
potential energy per unit weight =
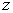
kinetic energy =
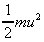
kinetic energy per unit weight =
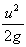
At any cross-section the pressure generates a force, the fluid will flow,
moving the cross-section, so work will be done. If the pressure at cross section
AB is p and the area of the cross-section is a then
force on AB =
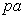
when the mass mg of fluid has passed AB, cross-section AB will have
moved to A'B'
volume passing AB =
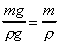
therefore
distance AA' =
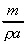
work done = force distance AA'
= 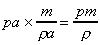
work done per unit weight =
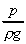
This term is know as the pressure energy of the flowing stream.
Summing all of these energy terms gives
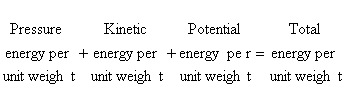
or
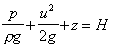
As all of these elements of the equation have units of length, they are often
referred to as the following:
pressure head =
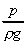
velocity head =
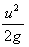
potential head =
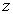
total head =
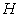
By the principle of conservation of energy the total energy in the
system does not change, Thus the total head does not change. So the
Bernoulli equation can be written
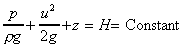
As stated above, the Bernoulli equation applies to conditions along a
streamline. We can apply it between two points, 1 and 2, on the streamline in
the figure below

Two points joined by a streamline
total energy per unit weight at 1 = total energy per unit weight at 2
or
total head at 1 = total head at 2
or
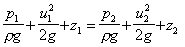
This equation assumes no energy losses (e.g. from friction) or energy gains
(e.g. from a pump) along the streamline. It can be expanded to include these
simply, by adding the appropriate energy terms:
|