

3. An example of the use of the Bernoulli
equation.
When the Bernoulli equation is combined with the continuity equation the two
can be used to find velocities and pressures at points in the flow connected by
a streamline.
Here is an example of using the Bernoulli equation to determine pressure and
velocity at within a contracting and expanding pipe.

A contracting expanding pipe
A fluid of constant density = 960
 is
flowing steadily through the above tube. The diameters at the sections are is
flowing steadily through the above tube. The diameters at the sections are
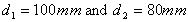 . The
gauge pressure at 1 is . The
gauge pressure at 1 is
 and
the velocity here is and
the velocity here is
 . We
want to know the gauge pressure at section 2. . We
want to know the gauge pressure at section 2.
We shall of course use the Bernoulli equation to do this and we apply it
along a streamline joining section 1 with section 2.
The tube is horizontal, with z1 = z2 so
Bernoulli gives us the following equation for pressure at section 2:

But we do not know the value of
 . We
can calculate this from the continuity equation: Discharge into the tube is
equal to the discharge out i.e. . We
can calculate this from the continuity equation: Discharge into the tube is
equal to the discharge out i.e.

So we can now calculate the pressure at section 2

Notice how the velocity has increased while the pressure has decreased. The
phenomenon - that pressure decreases as velocity increases - sometimes comes in
very useful in engineering. (It is on this principle that carburettor in many
car engines work - pressure reduces in a contraction allowing a small amount of
fuel to enter).
Here we have used both the Bernoulli equation and the Continuity principle
together to solve the problem. Use of this combination is very common. We will
be seeing this again frequently throughout the rest of the course.
4. Pressure Head,
Velocity Head, Potential Head and Total Head.
By looking again at the example of the reservoir with which feeds a pipe we
will see how these different heads relate to each other.
Consider the reservoir below feeding a pipe which changes diameter and rises
(in reality it may have to pass over a hill) before falling to its final level.

Reservoir feeding a pipe
To analyses the flow in the pipe we apply the Bernoulli equation along a
streamline from point 1 on the surface of the reservoir to point 2 at the outlet
nozzle of the pipe. And we know that the total energy per unit weight or
the total head does not change - it is constant - along a
streamline. But what is this value of this constant? We have the Bernoulli
equation

We can calculate the total head, H, at the reservoir,
 as
this is atmospheric and atmospheric gauge pressure is zero, the surface is
moving very slowly compared to that in the pipe so as
this is atmospheric and atmospheric gauge pressure is zero, the surface is
moving very slowly compared to that in the pipe so
 , so
all we are left with is , so
all we are left with is
 the
elevation of the reservoir. the
elevation of the reservoir.
A useful method of analysing the flow is to show the pressures graphically on
the same diagram as the pipe and reservoir. In the figure above the total
head line is shown. If we attached piezometers at points along the pipe,
what would be their levels when the pipe nozzle was closed? (Piezometers, as you
will remember, are simply open ended vertical tubes filled with the same liquid
whose pressure they are measuring).

Piezometer levels with zero velocity
As you can see in the above figure, with zero velocity all of the levels in
the piezometers are equal and the same as the total head line. At each point on
the line, when u = 0

The level in the piezometer is the pressure head and its value is
given by
 . .
What would happen to the levels in the piezometers (pressure heads) if the if
water was flowing with velocity = u? We know from earlier examples that
as velocity increases so pressure falls �

Piezometer levels when fluid is flowing

We see in this figure that the levels have reduced by an amount equal to the
velocity head,
 . Now
as the pipe is of constant diameter we know that the velocity is constant along
the pipe so the velocity head is constant and represented graphically by the
horizontal line shown. (this line is known as the hydraulic grade line). . Now
as the pipe is of constant diameter we know that the velocity is constant along
the pipe so the velocity head is constant and represented graphically by the
horizontal line shown. (this line is known as the hydraulic grade line).
What would happen if the pipe were not of constant diameter? Look at the
figure below where the pipe from the example above is replaced be a pipe of
three sections with the middle section of larger diameter

Piezometer levels and velocity heads with fluid flowing in varying
diameter pipes
The velocity head at each point is now different. This is because the
velocity is different at each point. By considering continuity we know that the
velocity is different because the diameter of the pipe is different. Which pipe
has the greatest diameter?
Pipe 2, because the velocity, and hence the velocity head, is the smallest.
This graphical representation has the advantage that we can see at a glance
the pressures in the system. For example, where along the whole line is the
lowest pressure head? It is where the hydraulic grade line is nearest to the
pipe elevation i.e. at the highest point of the pipe.
Losses due to friction.
In a real pipe line there are energy losses due to friction - these must be
taken into account as they can be very significant. How would the pressure and
hydraulic grade lines change with friction? Going back to the constant diameter
pipe, we would have a pressure situation like this shown below

Hydraulic Grade line and Total head lines for a constant diameter pipe
with friction
How can the total head be changing? We have said that the total head - or
total energy per unit weight - is constant. We are considering energy
conservation, so if we allow for an amount of energy to be lost due to friction
the total head will change. We have seen the equation for this before. But here
it is again with the energy loss due to friction written as a head and
given the symbol
 . This
is often know as the head loss due to friction. . This
is often know as the head loss due to friction.

|

