The general rules of statics (as applied in solid mechanics)
apply to fluids at rest. From earlier we know that:
- a static fluid can have no shearing force acting
on it, and that
- any force between the fluid and the boundary must be
acting at right angles to the boundary.
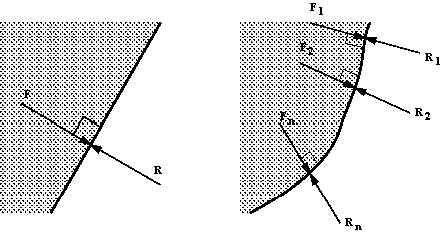
Pressure force normal to the boundary
Note that this statement is also true for curved surfaces, in
this case the force acting at any point is normal to the surface at that point.
The statement is also true for any imaginary plane in a static fluid. We use
this fact in our analysis by considering elements of fluid bounded by imaginary
planes.
We also know that:
- For an element of fluid at rest, the element will be in
equilibrium - the sum of the components of forces in any direction will be
zero.
- The sum of the moments of forces on the element about any
point must also be zero.
It is common to test equilibrium by resolving forces along
three mutually perpendicular axes and also by taking moments in three mutually
perpendicular planes an to equate these to zero.
As mentioned above a fluid will exert a normal force on any
boundary it is in contact with. Since these boundaries may be large and the
force may differ from place to place it is convenient to work in terms of
pressure, p, which is the force per unit area.
If the force exerted on each unit area of a boundary
is the same, the pressure is said to be uniform.
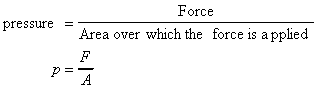
Units: Newton's per square metre,
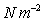 , ,
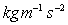 . .
(The same unit is also known as a Pascal, Pa, i.e. 1Pa = 1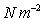 ) )
(Also frequently used is the alternative SI unit the bar,
where 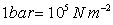 ) )
Dimensions:
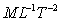 . .
(Proof that pressure acts equally in all directions.)
By considering a small element of fluid in the form of a
triangular prism which contains a point P, we can establish a relationship
between the three pressures px in the x direction, py in
the y direction and ps in the direction normal to the sloping face.
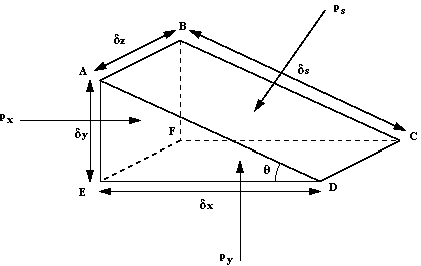
Triangular prismatic element of fluid
The fluid is a rest, so we know there are no shearing forces,
and we know that all force are acting at right angles to the surfaces .i.e.
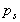 acts perpendicular to surface ABCD,
acts perpendicular to surface ABCD,
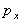 acts perpendicular to surface ABFE and
acts perpendicular to surface ABFE and
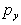 acts perpendicular to surface FECD.
acts perpendicular to surface FECD.
And, as the fluid is at rest, in equilibrium, the sum of the
forces in any direction is zero.
Summing forces in the x-direction:
Force due to
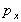 , ,
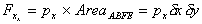
Component of force in the x-direction due to
 , ,

(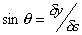 ) )
Component of force in x-direction due to
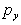 , ,
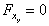
To be at rest (in equilibrium)
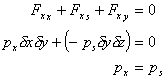
Similarly, summing forces in the y-direction. Force due to
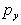 , ,
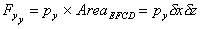
Component of force due to
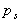 , ,
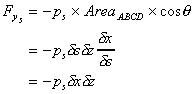
(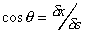 ) )
Component of force due to
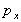 , ,
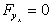
Force due to gravity,
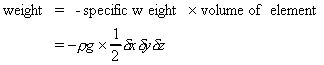
To be at rest (in equilibrium)
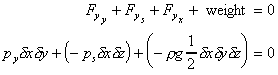
The element is small i.e.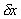 , ,
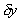 and and
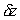 are
small, and so are
small, and so
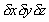 is
very small and considered negligible, hence is
very small and considered negligible, hence
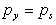
thus
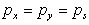
|