Forces on Submerged Surfaces in Static Fluids
We have seen the following features of statics fluids
- Hydrostatic vertical pressure distribution
- Pressures at any equal depths in a continuous fluid are
equal
- Pressure at a point acts equally in all directions
(Pascal's law).
- Forces from a fluid on a boundary acts at right angles to
that boundary.
Objectives:
We will use these to analyse and obtain expressions for the
forces on submerged surfaces. In doing this it should also be clear the
difference between:
- Pressure which is a scalar quantity whose value is equal
in all directions and,
- Force, which is a vector quantity having both magnitude
and direction.
Pressure is defined as force per unit area. If a pressure p
acts on a small area
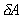 then
the force exerted on that area will be
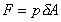
Since the fluid is at rest the force will act at right-angles
to the surface.
General submerged plane
Consider the plane surface shown in the figure below. The
total area is made up of many elemental areas. The force on each elemental area
is always normal to the surface but, in general, each force is of different
magnitude as the pressure usually varies.
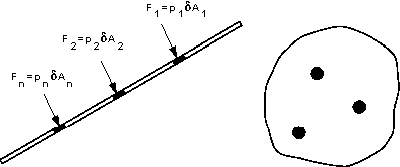
We can find the total or resultant force,
R, on the plane by summing up all of the forces on the small elements
i.e.
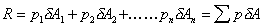
This resultant force will act through the centre of pressure,
hence we can say
If the surface is a plane the force can be
represented by one single resultant force,
acting at right-angles to the plane through the centre of pressure.
Horizontal submerged plane
For a horizontal plane submerged in a liquid (or a plane
experiencing uniform pressure over its surface), the pressure, p, will be
equal at all points of the surface. Thus the resultant force will be given by
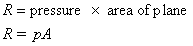
Curved submerged surface
If the surface is curved, each elemental force will be a
different magnitude and in different direction but still normal to the surface
of that element. The resultant force can be found by resolving all forces into
orthogonal co-ordinate directions to obtain its magnitude and direction. This
will always be less than the sum of the individual forces, .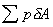
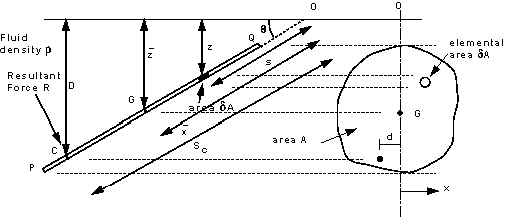
This plane surface is totally submerged in a liquid of density
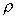 and
inclined at an angle of
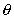 to
the horizontal. Taking pressure as zero at the surface and measuring down from
the surface, the pressure on an element
 ,
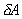submerged a distance z, is given by
and therefore the force on the element is
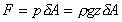
The resultant force can be found by summing all of these
forces i.e.
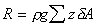
(assuming
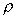 and
g as constant).
The term
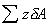 is
known as the 1st Moment of Area of the plane PQ about
the free surface. It is equal to
 i.e.
where A is the area of the plane and
 is the
depth (distance from the free surface) to the centroid, G. This can also be
written in terms of distance from point O ( as
 )
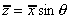Thus:
The resultant force on a plane
This resultant force acts at right angles to the plane through
the centre of pressure, C, at a depth D. The moment of R about any point
will be equal to the sum of the moments of the forces on all the elements
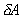 of
the plane about the same point. We use this to find the position of the centre
of pressure.
It is convenient to take moments about the point where a
projection of the plane passes through the surface, point O in the figure.
We can calculate the force on each elemental area:
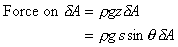
And the moment of this force is:
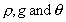are the same for each element, so the total moment is
We know the resultant force from above
 ,
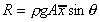which acts through the centre of pressure at C, so
Equating gives,
|
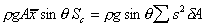
