Thus the position of the centre of pressure along the plane
measure from the point O is:
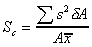
It look a rather difficult formula to calculate - particularly
the summation term. Fortunately this term is known as the 2nd
Moment of Area ,
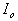 , of
the plane about the axis through O and it can be easily calculated for many
common shapes. So, we know: , of
the plane about the axis through O and it can be easily calculated for many
common shapes. So, we know:
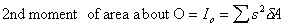
And as we have also seen that
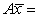 1st
Moment of area about a line through O, 1st
Moment of area about a line through O,
Thus the position of the centre of pressure along the plane
measure from the point O is:
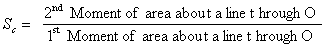
and depth to the centre of pressure is
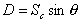
How do you calculate the 2nd moment of area?
To calculate the 2nd moment of area of a plane
about an axis through O, we use the parallel axis theorem together with
values of the 2nd moment of area about an axis though the centroid of
the shape obtained from tables of geometric properties.
The parallel axis theorem can be written
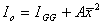
where
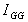 is
the 2nd moment of area about an axis though the centroid G of the
plane. is
the 2nd moment of area about an axis though the centroid G of the
plane.
Using this we get the following expressions for the position
of the centre of pressure
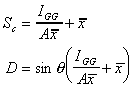
(In the examination the parallel axis theorem and the
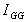 will
be given) will
be given)
The table blow given some examples of the 2nd
moment of area about a line through the centroid of some common shapes.
Lateral position of Centre of Pressure
If the shape is symmetrical the centre of pressure lies on the line of
symmetry. But if it is not symmetrical its position must be found by taking
moments about the line OG in the same way as we took moments along the line
through O, i.e.

but we have
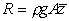 so so
|