| An Introduction To Circuit Analysis |
Electrical Circuits - An Introduction To Analytical Methods
Lesson Objectives
In this lesson you will encounter general
electrical circuits for the first time. You need to consider what you expect to
learn from this lesson. Here are our goals.
 Given a simple electrical circuit,
Given a simple electrical circuit,
 Be able to write the node equations for the circuit.
Be able to write the node equations for the circuit.
 Be able to write the loop equations for the circuit.
Be able to write the loop equations for the circuit.
 Be able to know which of the two approaches above are appropriate in any
given situation.
Be able to know which of the two approaches above are appropriate in any
given situation.
 Be able to solve the resulting equations to determine voltages and/or
currents in the circuit.
Be able to solve the resulting equations to determine voltages and/or
currents in the circuit.
Circuits
There are a number of tools you can use
for very small electrical circuits. For example, given a small electrical
circuit you can do any or all of the following.
- Look for resistor
combinations - either series or parallel,
- Look for sourcesthat
you can find a Thevinin or Norton equivalent for,
- Look for embedded
voltage dividers,
- Hope
that all of the above will lead to a very simple circuit that you can
analyze.
But - - - what happens when you do all of
that and you still can't figure out what goes on?
- You need some general method
that you know will get you to a result.
In other words, what you may need is a method
that has a high probability of success - one that is almost guaranteed to work
for a large variety of circuits. There are two general methods you might try in
that situation:
- The method of node voltages,
- The loop equation method.
In this lesson you will begin to learn some
general methods for analysis of electrical circuits. When you learn those
analysis methods you will have increased the number of tools in you analysis
toolbox. We ask you to be thoughtful as you do that. If your regular toolbox
is empty and someone gives you a hammer, then pretty soon everything will start
to look like a nail. Not only do you have to learn the tools for analysis, you
also have to learn when you need to use them, and
how to choose from the tools in your toolbox.
Node Voltage Equations
We are going to start with the method of
Node Voltages. The name of the method tells you
exactly what you are going to do.
- The method of
Node Voltages starts with
writing the KCL equations for the nodes in a circuit. Those equations are
written in terms of node voltages (even though you are writing the Current
Law, the variables are voltages!) thus the name!
That's a little simplified, but that is the
essence of the method. We'll start with a simple circuit, and we will try to
discover what you have to do. Here's a very simple circuit. It is a
voltage divider. We notice some very simple facts
about this circuit.
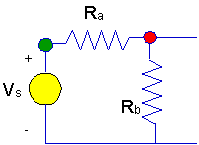
- There are two nodes in this
circuit. One is marked with a red dot, the other is marked with an green
dot.
- There is a difference between
the two nodes. If we know Vs - the source voltage - then
we know the voltage at the node marked with an green dot.
- We don't know the voltage at
the node marked with a red dot unless we do some analysis.
Now, what we are really saying about this
circuit is the following.
- Since there is only one node
where we do not know the voltage, when we write the equations for this
circuit, we really only need one equation.
- There's
one unknown and there's
going to beone equation.
- The equation we need to write
is KCL at the node with the unknown voltage
Now, we will write the equation at the node
with the unknown voltage.
- We need to define a
symbol for the unknown voltage. We'll call it
Vx.
- Then we write KCL at the node
where Vx appears.
- Finally, we solve whatever
equation results from writing KCL.
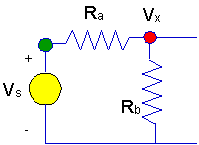
Now, we will write the equation at the
node with the unknown voltage.
- To write KCL we need to
define two currents for this case. They are shown below.
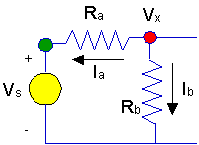
- Then KCL is written as:
- Ia
+ Ib = 0 since both
currents are leaving the node.
- We need to get
expressions forIa and
Ib. The expressions we need
are:
- Ia = (Vx
- Vs)/Ra
- Ib = (Vx
- 0)/Rb
In both cases the voltage across the resistor causing
the current to flow in the indicated direction is:
Voltage at the node - Voltage
at other resistor end.
- Note that one end of Rb
is connected to ground, so a zero appears in that expression.
- It is important to be sure
you understand how each current is calculated, and the exact expression for
the current. The current through a resistor, R, connected to a node is:
(Voltage at the node -
Voltage at other resistor end)/R
- Then, since:
- Ia = (Vx
- Vs)/Ra and
- Ib = (Vx
- 0)/Rb
- We can write the complete KCL
equation.
- KCL gives us:
Ia + Ib = 0.
- So, we have:
- (Vx - Vs)/Ra
+ (Vx - 0)/Rb = 0
Now, remember the algorithm for using node
voltages.
- Define a symbol for the
unknown voltage. We've done that.
- Write KCL at the node
where Vx appears. Done that also.
- Solve whatever equation
results from writing KCL. We need to do that.
We need to learn how you can solve these
kinds of equations. It's not hard to solve the equation we have:
(Vx - Vs)/Ra
+ (Vx - 0)/Rb = 0
The result is:
Vx = Vs*Rb/(Ra
+ Rb)
Actually, this circuit was pretty easy.

- This circuit has
one unknown node voltage.
- We wrote
one KCL equation.
- We had
one equation with one unknown.
Now, we'll look at a more complicated
circuit.
Here is a more complicated circuit. This
ladder circuit is more complex for one simple reason.
- This circuit has
two unknown node voltages.
- The nodes with unknown
voltages are marked with red dots.
- Once again, we have a
node where the voltage is known, and it is marked with an green dot.
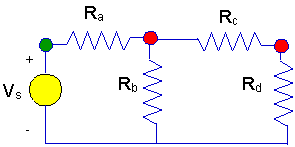
We use the same solution algorithm as
before.
- Define symbols for the
unknown voltages. We'll useVx
andVy.
- Then we write KCL at
the nodes whereVx
andVy
appear.
- Finally, we solve whatever
equations result from writing KCL.
For the first step:
- Define symbols for the
unknown voltage -Vx
andVy.
They are shown on the diagram below.
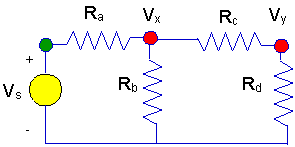
Vx
and Vy are shown at the
respective nodes. Notice again that the voltage and the node with the orange
dot is already know to be Vs
volts when measured with respect to ground.
For the second step:
- Write KCL at the nodes
where Vxand
Vyappear.
Again, currents need to be defined. Let's work on
node x first. Define currents as in the figure below, and write KCL.
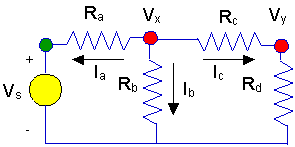
Ia+ Ib
+ Ic = 0.
- Then express each current in
terms of the node voltages.
- Ia = (Vx
- Vs)/Ra
- Ib = (Vx
- Vs)/Ra
- Ic = (Vx
- Vs)/Ra
So, if we put these current expressions into the KCL
equation, we get:
(Vx - Vs)/Ra
+ (Vx - Vs)/Ra + (Vx
- Vs)/Ra = 0
Now, we need to solve this equation. This is one
equation, but it has two unknowns, Vx
and Vy. We need a second
equation, and clearly it is obtained by writing KCL at node y. Writing KCL at
node y we get:
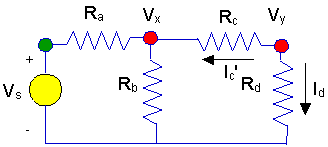
Ic' + Id
= 0
- We use
Ic'
because it is not the same asIc.
ActuallyIc' = - Ic.
- Still, using these
definitions, we get:
- Ic' =
(Vy - Vx)/Rc
- Id =(Vy
- 0)/Rd
Combining the expressions for the terms in KCL at
node y, we have:
(Vy - Vx)/Rc
+ (Vy - 0)/Rd = 0
And, the equation we had from node x is:
(Vx - Vs)/Ra
+ (Vx - 0)/Rb + (Vx - Vy)/Rc
= 0
Now, we're going to write out both equations and
combine Vx and
Vy terms. Here's the result of
rearranging the equations that way.
Vx(1/Ra+
1/Rb + 1/Rc) -Vy/Rc
= Vs/Ra
Vy(1/Rc+
1/Rd) - Vx/Rc = 0
These are close to what we want. We are
going to rearrange these equations to show the coefficients of
Vx and Vy
better next.
Vx(1/Ra+
1/Rb + 1/Rc) -Vy/Rc
= Vs/Ra
-Vx/Rc+
Vy(1/Rc+ 1/Rd) = 0
There are several things to note here,
even though we only have a set of equations to solve, and we haven't solved
those equations yet.. First, the equations can be easily obtained from the
circuit diagram. We'll work on that in a while, but you may already have
noticed that there is a kind of symmetry to the equations, and there are clear
relationships between the nodes the resistors are connected to, and how those
resistance values enter into the equations.
You may also have noted that the equations
that result are simultaneous linear equations.
Basically, you have two unknown node voltages, and the equations you write
result in two equations in those two unknown node voltages. You know everything
else in the equations, including resistance and source voltage values.
Finally, you may already know
several algorithms for solving simultaneous linear
equations.
|

