Here, a, b, c ....i, are known coefficients (either numerical or symbolic).  And, x, y and z are the unknown variables that we want to find.  The values, j, k and l are known values.  In a circuit, j, k and l would be the parts of the equation that contain independent voltage and current sources.

        The solution in this case is expressed in exactly the same way as it was for the system of two simultaneous equations:

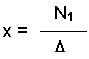However, in this case the determinants are determinants of 3 x 3 matrices - with 9 elements.  The characteristic determinant, D, looks like this: 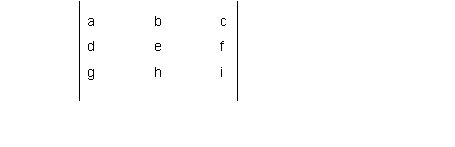You can see that there are now nine elements in the determinant.  The question is "How is the determinant calculated?".  In this case, the computation is notthe product of the two elements on the descending diagonal minus the product of the two elements on the ascending diagonal.  There are six terms in the expression for the determinant.: D = aei + bfg + cdh - gec -ahf - dbi

        The first term is the product of the three elements on the descending diagonal.  And, the three elements on the ascending diagonal are also multiplied together and they show up with a negative sign.  All of that is the same as the 2 x 2 case.  But, there are four more terms, and we need to understand them.  The animation below shows how the determinant is built from the elements within the matrix.

Note the following about this computation:

• In each term in the result, one coefficient is chosen from each row.
  • In the aei term,
  • a is in the first row,
  • e is in the second row and
  • i is in the third row.
• In each term in the result, one coefficient is chosen from each column.
  • In the aei term,
  • a is in the first column,
  • e is in the second column and
  • i is in the third column.
• Those conclusions about rows and columns are true for every term in the result.
• The result contains every possible way to choose one element from the first row, one from the second row, etc., and one from the first column, one from the second column, etc., without ever choosing two terms from the same row or column for any single term.
• The result can be interpreted as a sum of all the possible ways to choose terms from the main descending diagonal, and two sub-diagonals.  For example, the bfg term has b and f along a short "diagonal", and that term picks up the g term.  The cdh term also has two coefficients along a  short diagonal - d and h - and one coefficient  - c - to fill out that term.
• There is a system to the way signs are assigned.  Actually, the algorithm is that the sign depends upon whether the permutation of the coefficient indices is odd or even.
  • We will leave that to a math textbook.

• There are four ways to choose an element from the first column.
• After an element is chosen from the first column, there are three rows left from which an element could be chosen.  Thus, there arethree ways to choose an element from the second column.
• After an element is chosen from the second column, there are two rows left from which an element could be chosen.  Thus, there aretwo ways to choose an element from the third column.
• That leaves one way to choose an element from the fourth column.

• Conclusion:
  • There is no simple algorithm to visualize the determinant of a 4 x 4 matrix!