| Determinants |
Determinants
Determinants are important in many
different kinds of analysis. The most common way you can encounter determinants
is when solving simultaneous systems of linear
equations. Many analysis programs have the ability to do determinant
computations. However, it can be important to understand how to use
determinants, and there may be occasions when you want to be able use calculate
a small determinant. In this lesson we will review how determinants arise and
how small sets of simultaneous equations manually.
We start with a simple example. Assume
that you have two simultaneous linear equations in two unknowns, x and y. Here
are the equations:
a*x + b*y = e
c*x + d* y = f
You may know a number of ways to solve these
equations for x and y. However, here we are going to present the solution
method using determinants. The solution is easily stated:
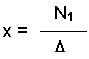
Similarly, the solution for y is given as:
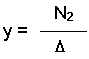Here, N1,
N2 and D
are all determinants. We will look at the denominator determinant,
D, first since it appears in the solution for
every variable. It is defined as:
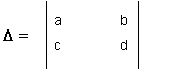
We say that "D
is the determinant of the system of equations". D
is computed from the coefficients of the variables (x and y) on the left hand
side of the set of equations. We can view this determinant as the determinant
of a matrix formed from those coefficients. This determinant is actually
computed as:
D = ad - cb
Paraphrasing this result we
see that D is the product of the two elements on the descending diagonal
(that is "a" times "d") minus the product of the two elements on the ascending
diagonal (that is "c" times "d").
The other two determinants,
N1 and N2,
are computed in the same way, but not with the same coefficients.
N1 is similar to
D but for N2
the first column is replaced by the values on the right hand side of the set of
equations. This means:
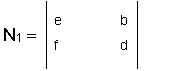So, we find:
N1 = ed - fb
which is computed in exactly the same manner as
D was computed.
In any event, we can note the following:
- We have the
solution for x:
- We can also compute the
solution for y.
However, in the set of equations y appears in the second column, so to
compute N2 we replace the
second column in D, and then compute the
determinant.
- The
characteristic determinant, D,
appears in the denominator of the solution for every variable.
- The method can be a numerical
method or a symbolic method. In other words, you can use the technique with
numerical coefficients, or with symbolic coefficients.
|
