| An Introduction To Fourier Analysis |
Experiments
E1
In the demo above, do the following.
- Start with a single term
in the series and plot the response. A single term should give you a
sine wave signal with an amplitude of 1.0.
- Slowly increment the
number of terms so that you include the third harmonic (two terms), the
fifth harmonic (three terms), etc.
- Does the peak value
increase or decrease as you increase the number of terms?
- Determine if you can get
the series to a point where the approximation is always within 5% of the
ideal square wave.
- When the series looks
like it has converged, determine the value of the square wave
amplitude. Compare that to the amplitude of the sine wave you started
with in the first step.
Let's examine another case. Here is
another simulator. However, here the function that is implemented is given by
the sum below.

Experiments
E2
In the demo above, do the following.
- Start with a single term
in the series and plot the response. A single term should give you a
sine wave signal with an amplitude of 1.0.
- Slowly increment the
number of terms so that you include the third harmonic (two terms), the
fifth harmonic (three terms), etc.
- Does the function
approach a square wave.
- Is there anything you
notice about the approximation, especially near the discontinuity?
Calculating The Fourier
Series Coefficients
At this point there are a few questions
that we need to address. Here are some questions that need to be answered.
- What kind of functions can be
represented using these types of series?
- Actually, most periodic
signals can be represented with a series composed of sines and cosines.
Even discontinuities (like in the square wave function or the sawtooth
function in the simulations) will not present an insurmountable problem,
although you might expect (from the simulation results) that there are
some phenomena we need to account for right at the discontinuities.
- How do you figure out what
the series is for any given function?
- That's an interesting
question, and we will discuss that soon. There are some mathematical
results we will need, but you should be prepared for that.
- Are there any practical
implications to all of this?
- Since functions can be
thought of as being composed of sines at cosines at different
frequencies, and since various linear systems process sinusoidal signals
in a way that is frequency dependent, these two facts mean that the
response of a system with a periodic input can be predicted using
frequency response methods.
- Many signals are now
analyzed using frequency component concepts. Special computational
techniques (particularly the FFT, or Fast Fourier Transform) have been
developed to calculate frequency components quickly for various
signals. Signals that have been analyzed include sound signals in
earthquakes, bridge vibrations under dynamic load (as well as stress
vibrations in many different structures from tall buildings to aircraft
vibrations) and communication signals (including the signals themselves
as well as the noise that interferes with the signals).
Now, let's try to answer some of these questions,
starting with the computation of the frequency components.
In general, a periodic signal can be
represented as a sum of both sines and cosines. Also, since sines and cosines
have no average term, periodic signals that have a non-zero average can have a
constant component. Altogether, the series becomes the one shown below. This
series can be used to represent many periodic functions. The function, f(t), is
assumed to be periodic.
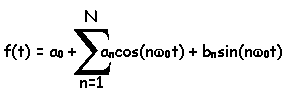
The coefficients, an and bn,
are what you need to know to generate the signal.
To compute the coefficients we take
advantage of some properties of sinusoidal signals. The starting point is to
integrate a product of f(t) with one of the sinusoidal components as shown
below.

Now, if we assume that the function, f(t), can be
represented by the series above, we can replace f(t) with the series in the
integral.
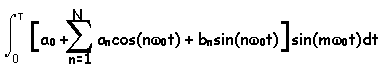
Here, we note the following:
Then, when we do the integration, we can use some
properties of the sinusoidal functions. In all cases here, the integral is take
over exactly one period of the periodic signal, f(t).


So, when we do the integration of the function,
f(t), multiplied by any sine or cosine function, they almost all work out to be
zero. The only one that doesn't work out to be zero is the one where n and m
are equal.
 Realizing all of this, we can conclude:
Realizing all of this, we can conclude:
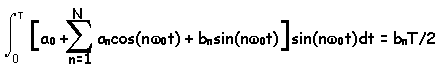 or:
or:

Which gives us a way to compute any of the b's in
the Fourier Series.
At this point we have half of our problem
solved because we can compute the b's, but we still need to compute the a's.
However, we can do the same thing for the a's that we did for the b's (and we
will let you do that yourself) and we get the following expressions for the
coefficients.
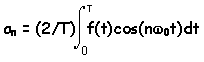
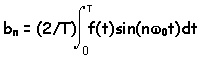 and these expressions are good for n>0 and m> 0. The
only coefficient not covered is ao which is given by:
and these expressions are good for n>0 and m> 0. The
only coefficient not covered is ao which is given by:
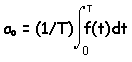
So, now we have a way to find all of the
coefficients in a Fourier Series expansion. Let us apply what we know to an
example.
Example/Experiment
E3
We will compute the Fourier Series of a general pulse that repeats. The pulse
sequence is shown below. The pulse signal varies between zero volts and one
volt.

Now, to evaluate the coefficients,
we do the integrations indicated above. We have the following.
 or:
an =
2Asin(nwoTp)/(nTwo)
or:
an =
2Asin(nwoTp)/(nTwo)
an =
Asin(nwoTp)/(np)
Similarly,
 or:
bn =
2A[-cos(nwoTp)
+ 1]/(nTwo)
or:
bn =
2A[-cos(nwoTp)
+ 1]/(nTwo)
bn =
A[-cos(nwoTp)
+ 1]/(np)
and,
ao = (Tp/T)
Now, we can compute some of the
coefficients for a particular case. We will examine the situation where the
pulse is high for one-fourth of the period, i.e. when Tp =
T/4. In that situation we have:
nwoTp
= (n2p/T)Tp
= np/2
Note that the a's (the cosine
coefficients) will all be zero for even n's, while the b's (the sine
coefficients) will be zero for every fourth n. That being said, the
coefficients we have computed are given in the table below. For this table we
have assumed a period of 4 seconds. We'll show that later in a real-time
simulator.
| n
|
an
|
bn
|
| 0
|
.25
|
-
|
| 1
|
.31831
|
.31831
|
| 2
|
0
|
.31831
|
| 3
|
-.10610
|
.10610
|
| 4
|
0
|
0
|
| 5
|
.06366
|
.06366
|
| 6
|
0
|
.10610
|
| 7
|
-.04547
|
.04547
|
| 8
|
0
|
0
|
| 9
|
.03537
|
.03537 |
| 10
|
0
|
.06366 |
Now, we can check whether these
coefficients actually produce a pulse. Here is a real-time simulator that will
let you check that. It has been pre-loaded with the coefficients we calculated
above to produce a pulse. However, since we are only using harmonics up to the
10th harmonic, it will not be an exact representation.
Run the simulator to check
whether we are close. Then do the following.
Questions/Problems
Using the simulator,
answer the following questions
Q1
Does the waveform with 10 harmonics look like - with more harmonics - it will
converge to the pulse we started with?
P1
Determine the average value (i.e. DC component) of the signal.
|

