Fourier Series

Experiments

E2   In the demo above, do the following.

• Start with a single term in the series and plot the response.  A single term should give you a sine wave signal with an amplitude of 1.0.

• Slowly increment the number of terms so that you include the third harmonic (two terms), the fifth harmonic (three terms), etc.

• Does the function approach a square wave.

• Is there anything you notice about the approximation, especially near the discontinuity?

Calculating The Fourier Series Coefficients

       At this point there are a few questions that we need to address.  Here are some questions that need to be answered.

• What kind of functions can be represented using these types of series?

• Actually, most periodic signals can be represented with a series composed of sines and cosines.  Even discontinuities (like in the square wave function or the sawtooth function in the simulations) will not present an insurmountable problem, although you might expect (from the simulation results) that there are some phenomena we need to account for right at the discontinuities.

• How do you figure out what the series is for any given function?

• That's an interesting question, and we will discuss that soon.  There are some mathematical results we will need, but you should be prepared for that.

• Are there any practical implications to all of this?

• Since functions can be thought of as being composed of sines at cosines at different frequencies, and since various linear systems process sinusoidal signals in a way that is frequency dependent, these two facts mean that the response of a system with a periodic input can be predicted using frequency response methods.

• Many signals are now analyzed using frequency component concepts.  Special computational techniques (particularly the FFT, or Fast Fourier Transform) have been developed to calculate frequency components quickly for various signals.  Signals that have been analyzed include sound signals in earthquakes, bridge vibrations under dynamic load (as well as stress vibrations in many different structures from tall buildings to aircraft vibrations) and communication signals (including the signals themselves as well as the noise that interferes with the signals).

Now, let's try to answer some of these questions, starting with the computation of the frequency components.

        In general, a periodic signal can be represented as a sum of both sines and cosines.  Also, since sines and cosines have no average term, periodic signals that have a non-zero average can have a constant component.  Altogether, the series becomes the one shown below.  This series can be used to represent many periodic functions.  The function, f(t), is assumed to be periodic.

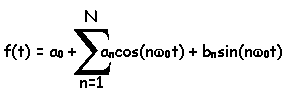
The coefficients, a_n and b_n, are what you need to know to generate the signal.

        To compute the coefficients we take advantage of some properties of sinusoidal signals.  The starting point is to integrate a product of f(t) with one of the sinusoidal components as shown below.

Now, if we assume that the function, f(t), can be represented by the series above, we can replace f(t) with the series in the integral.

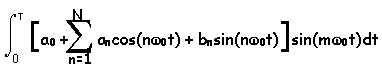
Here, we note the following:

• f = 1/T,

• w_o= 2pf.

Then, when we do the integration, we can use some properties of the sinusoidal functions.  In all cases here, the integral is take over exactly one period of the periodic signal, f(t).

So, when we do the integration of the function, f(t), multiplied by any sine or cosine function, they almost all work out to be zero.  The only one that doesn't work out to be zero is the one where n and m are equal.

Realizing all of this, we can conclude:

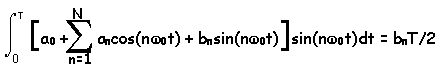
or:

Which gives us a way to compute any of the b's in the Fourier Series.

        At this point we have half of our problem solved because we can compute the b's, but we still need to compute the a's.  However, we can do the same thing for the a's that we did for the b's (and we will let you do that yourself) and we get the following expressions for the coefficients.

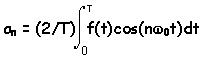
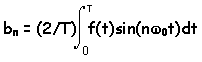
and these expressions are good for n>0 and m> 0.  The only coefficient not covered is a_o which is given by:

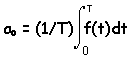
So, now we have a way to find all of the coefficients in a Fourier Series expansion.  Let us apply what we know to an example.

E3      We will compute the Fourier Series of a general pulse that repeats.  The pulse sequence is shown below.  The pulse signal varies between zero volts and one volt.

Now, to evaluate the coefficients, we do the integrations indicated above.  We have the following.

or:

Similarly,

or:

and,

Now, we can compute some of the coefficients for a particular case.  We will examine the situation where the pulse is high for one-fourth of the period, i.e. when T_p = T/4.  In that situation we have:

Note that the a's (the cosine coefficients) will all be zero for even n's, while the b's (the sine coefficients) will be zero for every fourth n.  That being said, the coefficients we have computed are given in the table below.  For this table we have assumed a period of 4 seconds.  We'll show that later in a real-time simulator.
 

Now, we can check whether these coefficients actually produce a pulse.  Here is a real-time simulator that will let you check that.  It has been pre-loaded with the coefficients we calculated above to produce a pulse.  However, since we are only using harmonics up to the 10^th harmonic, it will not be an exact representation.

Questions/Problems

        Using the simulator, answer the following questions

Q1   Does the waveform with 10 harmonics look like - with more harmonics - it will converge to the pulse we started with?

Example/Experiment

E4      Next, we will compute the Fourier Series of a triangle wave, as pictured below.

Now, to evaluate the coefficients, we need to do the integrations indicated above.  However, we know a few things about this function.

• The triangle function above is even.  In other words, if T(t) is the triangle signal above.

• T(t) = T(-t).

• Since the function is even, there can be no odd functions in the Fourier expansion.

• In other words, there are not sine terms since sin(x) = -sin(-x), i.e. the sine function is odd.

• The triangle function above has odd symmetry around the quarter period point.  In other words, if you look at the wave as though it were centered at t = T/4, you find odd symmetry.  Even harmonic cosine functions have even symmetry around this point.  (That would be the second harmonic cosine, the fourth harmonic cosine, etc.)  In this figure, you can see the triangle wave, a second harmonic cosine wave, and the product of the two.  The product of the even harmonic cosine signal and this triangle signal do not have any net area - in a period, or even in half a period.

• The conclusion that we reach is that there will be no even harmonic cosine terms.  Since there are no sine terms whatsoever, that means that the entire Fourier Series is composed of odd harmonic cosines only.  Thus, we need only compute those terms.

• Doing the computation, we note that we need only do the computation for one half of a period, and double the result.



• The result is:  (NOTE:  You can check the integral as a problem for the interested student.)

• b_k = 8A/(p²k²) as long as k is oddb_k = 0 for even k.

       At this point you have the basic knowledge you need to compute Fourier Series representations for periodic signals.  Moreover, when you encounter the Fast Fourier Transform (FFT) you should be able to understand the concepts you will encounter there.  Fourier Series concepts are useful in their own right, but they are also the building blocks you need to be able to understand Fourier and laPlace transforms, and, in turn, those concepts are the fundamental concepts you need when you encounter linear systems and control systems.