What
are you trying to do in this lesson?
Here are some goals for this lesson

Given a signal as a time function,

Be able to compute the frequency components of the signal.

Be able to predict how the signal will interact with linear systems and
circuits using frequency response methods.
The
first goal is really to be able to express a periodic signal in frequency
response language. The second goal is to be able to take a frequency
representation of a signal and use that representation to predict how the
signal will interact with systems.
Why
Use Frequency Representations When We Can Represent Any Signal With Time
Functions?
Signals are functions of time. A frequency response representation is a
way of representing the same signal as a frequency function. Why bother
- especially when we can represent the signal as a function of time and
manipulate it any way we want there? For example,
-
In a system, if we have
the time function, we can solve an input-output differential equation to
get the output, and
-
We can plot functions
of time and get information about them, and
-
etc., etc.
Frequency response methods give a different
kind of insight into a system. Those
insights can have unexpected results.

Frequency methods focus on how signals of different frequencies are represented
in a signal. We think in terms of the spectrum
of the signal. Here is a rainbow. In a rainbow, white sunlight
- composed of many different colors or parts of the spectrum - is spread
into its spectrum. Here the atmosphere is a filter that treats the
different parts of the light spectrum - the different light frequencies
- in different ways. For a rainbow, the different parts of the light
spectrum - the different colors - are bent differently as they enter the
atmosphere. In many electrical circuits and systems, the different
parts of the signal spectrum are treated differently. Different
treatment of different parts of the electromagnetic spectrum means that
you can separate out different radio, television and cell phone signals.
That gives you one very strong reason to learn about frequency methods.
In a linear system, frequency methods may be easier to apply, and may give
insight you would not get otherwise.
-
In a system, if we have
the time function, we can solve an input-output differential
equation to get the output, but if we use
frequency-based methods we may only need to do some algebra
to get the output. Most of us would rather do algebra than solve
differential equations.
-
Information about frequency
content of a signal has often proved to give more insight into how to process
a signal to remove noise. Often it is easier to characterize the
frequency content of a noise signal than it is to give a time description
of the noise.
So,
give it a shot and try learning about frequency response methods. They
can save you time and money in the long run.
Goals:
What are you trying to do in this lesson?

Given a signal as a time function,

Be able to compute the frequency components of the signal.
 Be
able to predict how the signal will interact with linearsystems and circuits
using frequency response methods.
The
Fourier Series
Some
time ago, Fourier, doing heat transfer work, demonstrated that any periodic
signal can be viewed as a linear composition of sine waves. Lets look at
a periodic wave. Here is an example plot of a signal that repeats every
second.
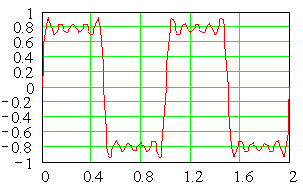
Clearly
this signal is not a sinusoid - and it looks as though it has no relationship
to sinusoidal signals. However, over a century ago, Fourier showed that
a periodic signal can always be represented as a sum of sinusoids (sines
and cosines, or sines with angles). That representation is now called a
Fourier Series in his honor.
Fourier not only showed that it was possible to represent
a periodic signal with sinusoids, he showed how to do it.
Assuming this signal repeats every T seconds, then we can describe it as
a sum of sinusoids. Here is the form of the sum. Fourier gave
an explicit way to get the coefficients in a Fourier Series and we need
to look at that in a while. First we are going to look at how a signal
can be built from a sum of sinusoids.
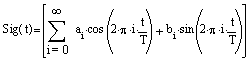
Here's that signal again. Is this signal
a sum of sinusoids? We will examine that question here now, starting with
a single sine signal.

Here is a single sine signal.
The expression for this signal is just:
Sig(t) = 1 * sin(2pt/T)
and T = 1 second.
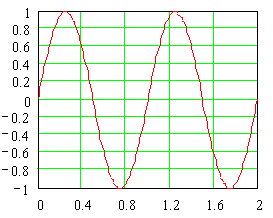
Now, we are going to add one other sine to
our original sine signal. The sine we add will be at three times the frequency
of the original and it will be one third as large.
Sig(t) = 1 * sin(2pt/T)
+ (1/3) * sin(6pt/T)
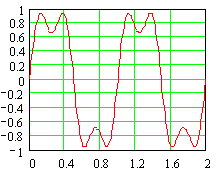
This looks a little different. Continue
by adding one more sine signal - at five times the original frequency and
one-fifth of the original size.
Sig(t) = 1 * sin(2pt/T)
+ (1/3) * sin(6pt/T)
+ (1/5) * sin(10pt/T)
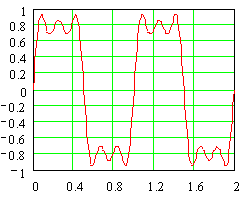
This is getting interesting. We are just adding
in terms at odd multiples of the original frequency. Here's what the signal
looks like with the terms up to the 11th multiple.
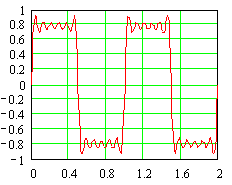
This looks like a fairly lousy square wave.
Let's add a lot more terms and see what happens.
Here is the signal with terms up to the
49th multiple.
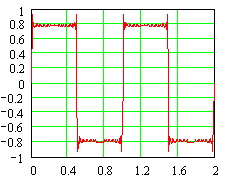
At
this point is seems that this process is giving us a signal that is getting
closer and closer to a square wave signal. However, this looks like
a fairly lousy square wave. Let's add a lot more terms and
see what happens.
Here is the signal with odd terms up to the 79th multiple. Now we're
getting a pretty clear indication of a square wave with an amplitude a
little under 0.8. In fact, the way we are building this signal we
are using Fourier's results. We know the formula for the series that
converges to a square wave.
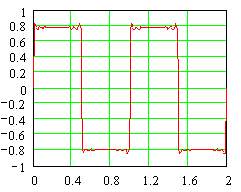
In fact, the way we are building this signal we are using Fourier's results.
We know the formula for the series that converges to a square wave.
Here's the formula. For a perfectly accurate representation, let N go to
infinity.
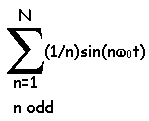
Now,
we're going to give you a chance to do this kind of experiment yourself.
Shown below is an interactive demo that will let you control the number
of terms in the summation above. In the demo you can also control
the frequency.
Experiments
E1 In
the demo above, do the following.
-
Start with a single term
in the series and plot the response. A single term should give you
a sine wave signal with an amplitude of 1.0.
-
Slowly increment the number
of terms so that you include the third harmonic (two terms), the fifth
harmonic (three terms), etc.
-
Does the peak value increase
or decrease as you increase the number of terms?
-
Determine if you can get
the series to a point where the approximation is always within 5% of the
ideal square wave.
-
When the series looks
like it has converged, determine the value of the square wave amplitude.
Compare that to the amplitude of the sine wave you started with in the
first step.
Let's examine another case.
Here is another simulator. However, here the function that is implemented
is given by the sum below.

|

