Frequency Dependent Circuits

• And, we know:

• And the second expression can be put into the form of the first

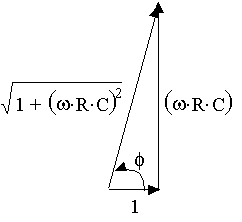
We need to refer to a little geometrical construction - at the right. "Clearly" we have the relationships indicated below for cos(f) and sin(f)

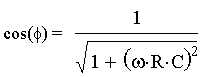
So, now we can write:

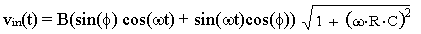
Which reduces to:

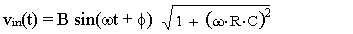
There are two conclusions to draw from the resulting expression for the input voltage.

• The ratio of the amplitude of the output to the input voltage is given by:

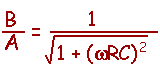
• The output voltage lags the input voltage by a phase angle, f.

You can use the expressions for the gain, B/A, and the phase shift, f

, to predict behvarior of circuits like this. You should note the following in these expressions.

• In the expression for B/A, there is a factor (wRC) which determines the attenuation. There is a "critical frequency" where that factor is 1. That frequency is:

• w= 1/RC

• or f = 1/2pRC

• When f = 1/2pRC the attenuation is 0.707 (the reciprocal of the square root of 2). You can consider that as the mid-point in freqency where the frequency is between the high frequency range (where the circuit does not pass a sinusoidal signal well) and the low frequency range (where a sinusoidal signal tends to pass through the filter unchanged).

• When f = 1/2pRC the phase is -45^o. That is halfway between the low frequency phase (which tends toward 0^o as the frequency tends to zero - i.e. DC) and the high frequency phase (which tends toward -90^o as the frequency gets very high).

• So, there are two reasons to think of that frequency (f = 1/2pRC) as a critical frequency.

• Note that that frequency is sometimes referred to as the bandwidth of the circuit. It's one way to measure the band of frequencies that get through the circuit relatively unscathed.

With those thoughts you can think a little more deeply using the simulator we have just below.

A Simulation of the Circuit

Note: - This simulator is real time. However, to let you see how the circuit behaves, we have made the signals very slow - on the order of a few Hertz, or even a fraction of a Hertz. The time constant (the R-C product) should be correspondingly long - on the order of a second (from a fraction of a second to a few seconds). You won't see much if you stray far from these limits - even though these are long time constants and the bandwidths are quite low. That's just for purposes of illustration. (However, note that you could get a one second time constant using R = 1.0 MW, and C = 1.0mf.)

Here is the simulator.

Using this simulator, you can do the following.

• You can change the frequency.

• Notice that higher frequencies are attenuated more. (The output is smaller.)

• Lower frequencies are attenuated less. (The output is larger.)

• You can change the time constant (The R-C product).

• Notice that higher time constants shift the bandwidth lower, and high frequencies are attenuated more.

• Lower time constants shift the bandwidth higher, and high frequencies are attenuated less. (The output is larger.) Actually, with lower time constants, the bandwidth is higher and more frequencies get through the circuit.

Reflections

In this lesson you have been introduced to a simple frequency dependent circuit. We have used a very brute-force method - assuming a voltage at the output and chasing that back to the input. That worked here, but it won't work everywhere. Moreover, this is not the easiest way to make such predictions, and before you attempt more complex circuits you should learn a better way to analyze frequency dependent circuits. You need to learn about impedance and phasors. There are links below that will take you to many other topics.