The LP formulation and the underlying
assumptions
A Linear Programming problem is a special case of a Mathematical
Programming problem. From an analytical perspective, a mathematical program
tries to identify an extreme (i.e., minimum or maximum) point of a
function
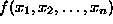, which furthermore satisfies a set of constraints, e.g.,
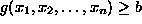. Linear programming is the specialization of mathematical programming to the
case where both, function f - to be called the objective function
- and the problem constraints are linear.
From an applications perspective, mathematical (and therefore, linear)
programming is an optimization tool, which allows the rationalization
of many managerial and/or technological decisions required by contemporary
techno-socio-economic applications. An important factor for the applicability of
the mathematical programming methodology in various application contexts, is the
computational tractability of the resulting analytical models. Under the advent
of modern computing technology, this tractability requirement translates to the
existence of effective and efficient algorithmic procedures able to provide a
systematic and fast solution to these models. For Linear Programming problems,
the Simplex algorithm, discussed later in the text, provides a powerful
computational tool, able to provide fast solutions to very large-scale
applications, sometimes including hundreds of thousands of variables (i.e.,
decision factors). In fact, the Simplex algorithm was one of the first
Mathematical Programming algorithms to be developed (George Dantzig, 1947), and
its subsequent successful implementation in a series of applications
significantly contributed to the acceptance of the broader field of
Operations Research as a scientific approach to decision making.
As it happens, however, with every modeling effort, the effective application
of Linear Programming requires good understanding of the underlying modeling
assumptions, and a pertinent interpretation of the obtained analytical solutions
|
