Table 2: Characteristics per pixel of some well-known cameras. Both
of the Photometrics camera are cooled using Peltier elements. Both were
evaluated in the 1x gain setting. The Sony camera is being used in integration
mode with integration times on the order of 3 to 4 seconds. (See [9].)
The extraordinary sensitivity of modern CCD cameras is clear from these data.
In the 1x gain mode of the Photometrics KAF 1400 camera, only 8 photoelectrons
(approximately 16 photons) separate two gray levels in the digital
representation of the image. For the considerably less expensive Sony camera
only about 500 photons separate two gray levels.
There are, of course, other possible sources of noise. Specifically:
- Readout noise - which can be reduced to manageable levels by slow
readout rates and proper electronics. At very low signal levels, however,
readout noise can become a significant component in the overall SNR.
- Amplifier noise - which is negligible with well-designed
electronics.
- Quantization noise - which is inherent in the digitization
process and yields an additive noise with SNR = 6b + 11 dB where b is the
number of bits. For b > 8 bits, this means a SNR > 59 dB. Quantization noise
can therefore be ignored when compared to the SNR's listed in Table 1 as the
total SNR of a complete system is dominated by the smallest SNR.
- Dark current - An additional, stochastic source of photoelectrons
is thermal energy. Electrons can be freed from the material itself through
thermal vibration and then, trapped in the CCD well, be indistinguishable
from "true" photoelectrons. By cooling the CCD chip to around -40 �C
it is possible to reduce significantly the number of "thermal electrons"
that give rise to dark current. Clearly, as the integration time T
increases, the number of thermal electrons increases. The probability
distribution of thermal electrons is also a Poisson process where the rate
parameter is an increasing function of temperature. It is straightforward to
measure this dark current and typical results for the three cameras are
presented in Table 2 [9]. There are alternative techniques (to cooling) for
suppressing dark current and these usually involve estimating the average
dark current for the given integration time and then subtracting this value
from the CCD pixel values before the A/D converter. While this does reduce
the dark current it also reduces the dynamic range of the camera.
All of this is of more than of academic interest when we consider the
strength of signals that are encountered in fluorescence microscopy. An example
is shown in Figure 8 [10].
 |
| (a) |
(b) |
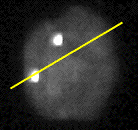
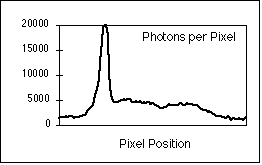
Figure 8: (a) Interphase nucleus stained for both general DNA (gray)
and centromeric DNA (white dots). Exposure time was 4 seconds with a
Photometrics KAF 1400 camera. (b) Number of photons per pixel along the yellow
line in (a).
Sampling Density
There are other sources of noise in a digital image besides noise
contamination of the pixel brightness. The act of sampling - cutting up the
image into rows and columns in 2D and rows, columns, and planes in 3D - is also
an important source of noise which is of particular significance when the goal
is image analysis. The potential effect of this kind of noise can be illustrated
with the relatively simple problem of measuring the area of a two dimensional
object such as cell nucleus. It has been known for many years [11] that the best
measure of the area of an "analog" object given its digital representation is to
simply count the pixels associated with the object. The use of the term "best
estimate" means that the estimate is unbiased (accurate) and that the variance
goes to zero (precise) as the sampling density increases. We assume here that
the pixels belonging to the object have been labeled thus producing a binary
representation of the object. The issue of using the actual gray values of the
object pixels to estimate the object area will not be covered here but can be
found in [12, 13].
To illustrate the issue let us look at a simple example. When a randomly
placed (circular) cell is digitized, one possible realization is shown in Figure
9. The equation for generating the "cell" is where R is the radius of the cell.
The terms ex and ey are independent random variables with
a uniform distribution over the interval (-1/2, +1/2). They represent the random
placement of the cell with respect to the periodic (unit) sampling grid.
Figure 9: Given small variations in the center position (ex,
ey) of the circle, pixels that are colored green will always remain
part of the object and pixels that are colored white will always remain part of
the background. Pixels that are shown in blue may change from object to
background or vice-versa depending on the specific realization of the circle
center (ex, ey) with respect to the digitizing grid.
In the realization shown in Figure 9 the area would be estimated at 84 pixels
but a slight shift of the circle with respect to the grid could change that, for
example, to 81 or 83 or 86. The sampling density of this figure can be expressed
as about 10 pixels per diameter. To appreciate what effect the finite sampling
density has on the area estimate let us look at the coefficient-of-variation of
the estimate, the CV =
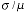 where where
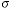 is the
standard deviation of the estimate of the area and � is the average estimate
over an ensemble of realizations. is the
standard deviation of the estimate of the area and � is the average estimate
over an ensemble of realizations.
If we denote the diameter of the cell by D and the size of a pixel as s x s,
then the sampling density is Q = D/s. The total area of the circle, A1,
that is always green (in Figure 9) independent of (ex, ey)
is given by:
 |
(6) |
The number of pixels associated with this is:
 |
(7) |
The total area of the region, Ab, that is blue (in Figure 9) is
given by:
 |
(8) |
and the number of pixels, Nb, associated with this region is:
 |
(9) |
The area of the circle is estimated by counting pixels and the contribution
from the green region is clearly N1. The total number will be NT
= N1 + n where n is a random variable. Let us make a simplifying
assumption: Let us assume that each of the pixels in the blue region can be part
of the object with probability p and part of the background with probability (1
- p) and that the decision for each pixel is independent of the other
neighboring pixels in the blue region. This, of course, describes a binomial
distribution for the pixels in that region. In fact this assumption is not true
and the behavior of neighboring pixels is somewhat correlated. But let us see
how far we can go with this model. Under this assumption:
 |
(10) |
and
 |
(11) |
We have made use of the assumption that N1 is deterministic - the
pixels are always green - and that the mean and variance of the binomial
distribution for Nb samples with probability p are given by Nb
p and Nb p(1 - p), respectively.
This immediately leads to an expression for the CV of our estimate as:
 |
(12) |
We can now study the convergence of the CV as the sampling density increases.
As Q increases in this two-dimensional image we have:
 |
(13) |
This type of argument can easily be extended to the three-dimensional case
where the results are:
 |
(14) |
and
 |
(15) |
Finally, for the N-dimensional case we have:
 |
(16) |
The conclusion is clear. As the sampling density Q increases the precision of
our estimates improve as a power of Q. While the independent binomial behavior
cannot be strictly true, the arguments presented do show the type of convergence
that can be expected and how that varies with Q. These results have also been
found experimentally in a number of publications [11-17]. An example in shown in
Figure 10. The measurement is the volume of spheres that have been randomly
placed on a sampling grid. The quality of the estimator (voxel counting) is
assessed by examining the CV.
Figure 10: For each sampling density value Q (expressed in voxels per
diameter), 16 spheres were generated with randomly placed centers (ex,
ey, ez). The volume was measured by counting voxels and
the CV(Q) =
 (Q) /
�(Q) calculated accordingly. (Q) /
�(Q) calculated accordingly.
It is clear from Figure 10 that as the sampling density increases by one
order of magnitude from Q=2 to Q=20 samples per diameter that the CV decreases
by two orders of magnitude. This illustrates the relation between CV and Q shown
in equation 15.
Choosing Sampling Density - We are now presented with an interesting
conundrum. Let us say we wish to measure the area of red blood cells. Their
individual diameters are on the order of 8.5 �m [18]. If we use a lens with NA =
0.75 and blue illumination with
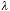 = 420
nm (near the absorption peak of hemoglobin), then according to equation 3 and
the Nyquist theorem, a sampling frequency of fs > 2 � fc =
7.2 samples per �m should be sufficient. This will give around 60 samples per
diameter which according to published results [14] should lead to more than
enough precision for biological work, that is, a CV below the 1% level. If,
however, a small chromosome as in Figure 4 is sampled with the same lens then
the approximate sampling density per chromosome "diameter" will be about 10
pixels and the CV above the 1% level. = 420
nm (near the absorption peak of hemoglobin), then according to equation 3 and
the Nyquist theorem, a sampling frequency of fs > 2 � fc =
7.2 samples per �m should be sufficient. This will give around 60 samples per
diameter which according to published results [14] should lead to more than
enough precision for biological work, that is, a CV below the 1% level. If,
however, a small chromosome as in Figure 4 is sampled with the same lens then
the approximate sampling density per chromosome "diameter" will be about 10
pixels and the CV above the 1% level.
The question then becomes should we choose the sampling density on the basis
of the Nyquist sampling theorem or on the basis of the required measurement
precision. The answer lies in the goal of the work. If we are interested in
autofocusing or depth-of-focus or image restoration then the Nyquist theorem
should be used. If, however, we are interested in measurements derived from
microscope images then the sampling frequencies derived from measurement
specifications (as exemplified in Figure 10 and equations 13, 15, and 16) should
be used.
Calibration
Finally, we come to the issue of using independent test objects and images to
calibrate systems for quantitative microscopy. In this section we will describe
procedures for calculating the actual sampling density as well as the effective
CV for specific measurements in a quantitative microscope system.
Sampling Density - A commercially prepared slide with a test pattern
(a stage micrometer or a resolution test chart) is, in general, necessary to
determine the sampling densities
 x and x and
 y in a
microscope system and to test whether the system has square pixels, that is, if y in a
microscope system and to test whether the system has square pixels, that is, if
 x = x =
 y. An
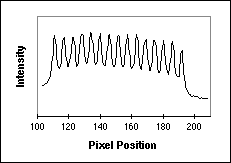
example of a digitized image of a test pattern is shown in Figure 11a and a
horizontal line through a part of the image is shown in Figure 11b. The image
comes from a resolution test chart produced by Optoline and taken in
fluorescence with a 63x lens and an NA = 1.4. y. An
example of a digitized image of a test pattern is shown in Figure 11a and a
horizontal line through a part of the image is shown in Figure 11b. The image
comes from a resolution test chart produced by Optoline and taken in
fluorescence with a 63x lens and an NA = 1.4.

 |
| (a) |
(b) |
Figure 11: (a) Fluorescence test pattern that can be used to measure
the sampling density. The yellow line goes through a series of bars that are
known to have a 2 �m center-to-center spacing (500 lp / mm). (b) The intensity
profile along the yellow line indicated on the left.
Using a simple algorithm we can process the data in Figure 11b to determine
that, averaged over 14 bars in the pattern, the sampling distance
 x = 2.9
samples / �m. By turning the test pattern 90� the sampling distance x = 2.9
samples / �m. By turning the test pattern 90� the sampling distance
 y can be
measured. Further, this test pattern can be used to compute the OTF [3, 19]. y can be
measured. Further, this test pattern can be used to compute the OTF [3, 19].
System performance - All measurement systems require standards for
calibration and quantitative microscopes are no exception. A useful standard is
prepared samples of latex microspheres. They can be stained with various
fluorescent dyes and they can also be used in absorption mode. An image of one
such microsphere is shown in Figure 12.
Figure 12: Fluorescently-labeled latex microsphere observed in
absorption mode with a Nikon Optiphot microscope and Nikon PlanApo 60x, NA=1.40
lens and digitized with a Cohu 4810 CCD camera and a Data Translation
QuickCapture frame grabber. The beads were from Flow Cytometry Standards Corp.
The sphere shown in Figure 12 comes from a population that is characterized
by the manufacturer as having an average diameter of 5.8 �m and a CV of 2%. We
can, therefore, use a population of these spheres to calibrate a quantitative
system. When measuring a population for a specific property (such as diameter),
we can expect a variation from sphere to sphere. The variation can be attributed
to the basic instrumentation (such as electronic camera noise), the experimental
procedure (such as focusing), and the "natural" variability of the microspheres.
Each of these terms is independent of the others and the total variability can
therefore be written as:
 |
(17) |
For a given average value of the desired property we have:
 |
(18) |
Through a proper sequence of experiments it is possible for us to assess the
contribution of each of these terms to the total CV. This total value will then
reflect the contributions from both of the effects described in detail above -
the various noise sources (quantum, thermal, electronic) as well as the effect
of the finite spatial sampling density.
As an example let us say that we wish to examine the CV associated with the
measurement of the diameter of the microspheres. The diameter of these spheres
can be estimated from the two-dimensional projected area of the spheres
according to the estimator:
 |
(19) |
We start with a single sphere placed in the center of the microscope
field-of-view and critically focused. An image is grabbed, corrected for the
deterministic variation of the background illumination, and then segmented to
provide a collection of labeled object pixels . The area and derived diameter
are then determined. We then repeat this procedure without moving the sphere
to acquire a total of N estimates of the diameter. For this protocol it is clear
that  proc
= proc
= 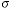 spher
= 0 and that only the variability associated with the equipment (the various
noise sources) will contribute to the total CV. When this technique was applied
with N=20 microspheres the result was CVtotal = CVequip =
0.1%. Note that this value is better than one might expect on the basis of the
SNR per pixel because a number of pixels were involved in determining the
diameter estimate. spher
= 0 and that only the variability associated with the equipment (the various
noise sources) will contribute to the total CV. When this technique was applied
with N=20 microspheres the result was CVtotal = CVequip =
0.1%. Note that this value is better than one might expect on the basis of the
SNR per pixel because a number of pixels were involved in determining the
diameter estimate.
We now take the same microsphere and move it out of the field-of-view
(in all three directions x, y, and z) and then back into the field at a random
position. This tests the variability associated with the sampling grid as well
as the effects of focusing while keeping
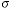 spher
= 0. When this procedure was repeated (N=20) the result was: spher
= 0. When this procedure was repeated (N=20) the result was:
 |
(20) |
which means that CVproc = 0.31%.
We are now ready to measure the total CV by looking at a population of
spheres. For N=185, the measured CVtotal = 1.41% which means that:
 |
(21) |
a value somewhat smaller than the manufacturer's specification. The results
are summarized in Figure 13.
Figure 13: The various coefficients-of-variation, CV's, associated
with the microsphere calibration protocols.
Summary
We have seen that modern CCD camera systems are limited by the fundamental
quantum fluctuations of photons that cannot be eliminated by "better" design.
Further, proper choice of the sampling density involves not only an
understanding of classic linear system theory - the Nyquist theorem - but also
the equally stringent requirements of digital measurement theory. Experimental
procedures that rely on the CV can be used to evaluate the quality of our
quantitative microscope systems and to identify which components are the
"weakest link." Typical values of relatively straightforward parameters such as
size can easily be measured to CV's around 1%.
Acknowledgments
This work was partially supported by the Netherlands Organization for
Scientific Research (NWO) Grant 900-538-040, the Foundation for Technical
Sciences (STW) Project 2987, and the Rolling Grants program of the Foundation
for Fundamental Research in Matter (FOM).
|

