Another direct consequence of the bandlimited nature of the microscope optics
can be found in procedures for autofocusing as well as for understanding the
issue of depth-of-focus. When an image specimen with Fourier spectrum I( x, x, y)
is passed through a microscope with an OTF given by H( y)
is passed through a microscope with an OTF given by H( x, x, y)
this produces an output image O( y)
this produces an output image O(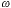 x, x,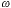 y) y)
= I(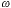 x, x,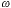 y)•H( y)•H(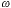 x, x,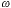 y).
The act of focusing or defocusing the microscope does not change the spectrum of
the specimen but rather the OTF. In other words the OTF is a function of the
z-axis position of the microscope. We can make this explicit by writing H( y).
The act of focusing or defocusing the microscope does not change the spectrum of
the specimen but rather the OTF. In other words the OTF is a function of the
z-axis position of the microscope. We can make this explicit by writing H(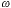 x, x,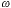 y, y,
 z).
A typical example of this dependency is shown in Figure 5. z).
A typical example of this dependency is shown in Figure 5.
Figure 5: As we move away from optimum focus, as
 z
increases, the H( z
increases, the H(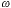 r)
"sags". These measured data describe a 60x lens with an NA of 1.4
(oil-immersion), and a wavelength of r)
"sags". These measured data describe a 60x lens with an NA of 1.4
(oil-immersion), and a wavelength of
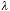 = 400 nm (blue). The cutoff frequency fc (from equation 3) should be
7.0 cycles per µm.
= 400 nm (blue). The cutoff frequency fc (from equation 3) should be
7.0 cycles per µm.
It is clear that independent of the focus H(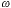 =0, =0,
 z)
= 1.0; all the light that enters the microscope through the objective lens is
assumed to leave the microscope through the ocular or camera lens. At the
bandlimit of the lens, the amplitude of H( z)
= 1.0; all the light that enters the microscope through the objective lens is
assumed to leave the microscope through the ocular or camera lens. At the
bandlimit of the lens, the amplitude of H(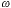 = =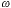 c, c,
 z)
= 0.0, again independent of focus. Thus autofocus algorithms can only expect to
work well when they examine midband frequencies around z)
= 0.0, again independent of focus. Thus autofocus algorithms can only expect to
work well when they examine midband frequencies around
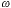 r
/ 2a = 0.75 (as seen in Figure 3b) and when the input signal spectrum I( r
/ 2a = 0.75 (as seen in Figure 3b) and when the input signal spectrum I(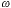 x, x,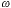 y)
contains a sufficient amount of energy in that spectral band. A complete
analysis of this can be found in [5]. y)
contains a sufficient amount of energy in that spectral band. A complete
analysis of this can be found in [5].
Further, the depth-of-focus - that distance
 z
over which the image specimen can be expected to be observed without significant
optical aberration - can be derived from considerations of wave optics and shown
to be [6, 7]: z
over which the image specimen can be expected to be observed without significant
optical aberration - can be derived from considerations of wave optics and shown
to be [6, 7]:
 |
(4) |
Again using the typical values of
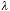 = 500 nm, NA = 1.4, and n = 1.5, we arrive at a depth-of-focus of
= 500 nm, NA = 1.4, and n = 1.5, we arrive at a depth-of-focus of
 z
= 0.13 µm, a very thin region of critical focus. z
= 0.13 µm, a very thin region of critical focus.
Photons - A second and equally important aspect of the physical signal
that we observe is the quantum nature of light. Assuming for the moment an ideal
situation, a single photon that arrives at a single CCD camera pixel may have
been transmitted through a specimen (as in absorptive microscopy) or may been
emitted by a fluorescent dye molecule. In either case that single photon for
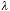 = 500 nm will carry an energy of E = h
= 500 nm will carry an energy of E = h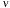 = hc/
= hc/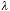 = 3.97 x 10-19 Joules. While this is a seemingly infinitesimal amount
of energy, modern CCD cameras are sensitive enough to be able to count
individual photons. The real problem arises, however, from the fundamentally
statistical nature of photon production. We cannot assume that in a given pixel
for two consecutive but independent observation intervals of length T that the
same number of photons will be counted. Photon production is governed by the
laws of quantum physics which restrict us to talking about an average number of
photons within a given observation window. The probability distribution of
photons in an observation window of length T seconds is known to be Poisson.
[8]. That is, the probability of p photons in an interval of length T is given
by:
= 3.97 x 10-19 Joules. While this is a seemingly infinitesimal amount
of energy, modern CCD cameras are sensitive enough to be able to count
individual photons. The real problem arises, however, from the fundamentally
statistical nature of photon production. We cannot assume that in a given pixel
for two consecutive but independent observation intervals of length T that the
same number of photons will be counted. Photon production is governed by the
laws of quantum physics which restrict us to talking about an average number of
photons within a given observation window. The probability distribution of
photons in an observation window of length T seconds is known to be Poisson.
[8]. That is, the probability of p photons in an interval of length T is given
by:
 |
(5) |
where
 is the rate or intensity parameter measured in photons per second. It is
critical to understand that, even if there were no other noise sources in the
imaging chain, the statistical fluctuations associated with photon counting over
a finite time interval T would still lead to a finite signal-to-noise ratio
(SNR). If we express this SNR as 20 log�10(
is the rate or intensity parameter measured in photons per second. It is
critical to understand that, even if there were no other noise sources in the
imaging chain, the statistical fluctuations associated with photon counting over
a finite time interval T would still lead to a finite signal-to-noise ratio
(SNR). If we express this SNR as 20 log�10( ),
then due to the fact that the average value of a Poisson process is given by µ = ),
then due to the fact that the average value of a Poisson process is given by µ =
 and the standard deviation is given by
and the standard deviation is given by
 ,
we have that SNR = 10 log�10( ,
we have that SNR = 10 log�10( ). ).

 |
| (a) |
(b) |
Figure 6: (a) Top: Gray level step wedge with 8 levels. Bottom: The
same step wedge as if each pixel were contaminated with Poisson noise and the
rate parameter
 was the original pixel value (with T=1 in eq. 5). (b) Two curves: the heavy
curve shows a horizontal line through the uncontaminated step wedge; the thin
line shows the result of the Poisson noise contamination.
was the original pixel value (with T=1 in eq. 5). (b) Two curves: the heavy
curve shows a horizontal line through the uncontaminated step wedge; the thin
line shows the result of the Poisson noise contamination.
In this context it is important to understand that the three traditional
assumptions about the relationship between signal and noise do not hold:
- the noise is not independent of the signal;
- the noise is not Gaussian, and;
- the noise is not additive.
Techniques that have been developed to deal with noisy images under the
traditional assumptions - techniques for enhancement, restoration, segmentation,
and measurement - must be reexamined before they can be used with these types of
images.
Camera Evaluation
Thinking in terms of photons has a direct effect on the evaluation of
alternative camera systems for quantitative microscopy. When a photon strikes
the photosensitive surface of a CCD, it may or may not cause a photoelectron to
be collected in the potential well. The probability of this happening is
associated with the quantum efficiency of the material (usually silicon) and the
energy (wavelength) of the photon. Typical values for the quantum efficiency for
silicon are around 50%, increasing towards the infra-red and decreasing towards
the blue end of the spectrum. But each photoelectron that is produced comes from
one photon so that photoelectrons (as well as photons) have a Poisson
distribution. If a CCD well has a finite capacity for photoelectrons, C, then
the maximum possible signal will be C and the standard deviation will be
 .
This means that the maximum SNR per pixel will be limited to SNR�max
= 10 log�10(C). Thus even if all other sources of noise are
negligible compared to the fundamental fluctuations in the photon counts, the
SNR will be limited by the CCD well capacity. If we choose to perform on-chip
integration after the well is full then we will only achieve blooming - the
leaking of the overfull well into other nearby wells. For three, well-known CCD
chips these limits are given in Table 1. .
This means that the maximum SNR per pixel will be limited to SNR�max
= 10 log�10(C). Thus even if all other sources of noise are
negligible compared to the fundamental fluctuations in the photon counts, the
SNR will be limited by the CCD well capacity. If we choose to perform on-chip
integration after the well is full then we will only achieve blooming - the
leaking of the overfull well into other nearby wells. For three, well-known CCD
chips these limits are given in Table 1.
| Chip
Manufacturer |
Pixel Sizeµm�2
|
Capacityphotoelectrons
|
SNRmaxdB
|
| Kodak KAF 1400 |
6.8 x 6.8 |
32,000 |
45 |
| Sony PA-93 |
11.0 x 11.0 |
80,000 |
49 |
| Thompson TH 7882 |
23.0 x 23.0 |
400,000 |
56 |
Table 1: Characteristics per pixel of some well-known
CCD chips.
Each of these chips when integrated into a well-designed camera is capable of
achieving these theoretical, maximum SNR values [9]. The invariant among these
three chips is the photoelectron capacity per square micron. If we think of the
well as having a volume given by the cross-sectional area times the depth, then
the capacity per unit cross-sectional area for all three chips is about 700
photoelectrons/µm�2.
The verification that the SNR is photon-limited can be achieved by looking at
the form of SNR(C) versus C. When the form is log(C) and the asymptotic value is
that given in Table 1, then we can be confident that we are dealing with a
well-designed camera that is, in fact, limited only by photon noise. An example
of this type of result for a Photometrics CC200 camera based on the Kodak KAF
1400 chip is given in Figure 7.
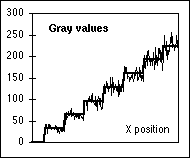
Figure 7: : SNR as a function of the recorded image brightness for a
cooled Photometrics KAF 1400 camera. The data were collected in both the 1x and
4x gain modes. The data follow a log(•) function (shown in a thick gray line) up
to the maximum well capacity of the CCD photoelement.
Using the Poisson model it is also possible to determine the sensitivity of
each camera. There is clearly a scale factor (G) between photoelectrons (e-
) and ADU. (An ADU is the step size of the A/D converter. That is, the
difference between gray level k and k+1.) Thus the output y (in ADU) and the
input x (in photoelectrons) are related by y = G•x. It holds for any random
variable that E{y} = E{G•x} = G•E{x} and V{y} = V{G•x} = G2•V{x}
where E{•} and V{•} are the expectation and variance operators, respectively.
Using the additional constraint that x has a Poisson distribution gives E{y} =
G•E{x} = G• and V{y} = G2•V{x}= G2•
and V{y} = G2•V{x}= G2• .
This means that an estimate of the scale factor is given by V{y} / E{y} = G
independent of .
This means that an estimate of the scale factor is given by V{y} / E{y} = G
independent of
 .
The sensitivity S is simply 1/G. The sensitivity for the three chips mentioned
above and in specific camera configurations is given in Table 2. .
The sensitivity S is simply 1/G. The sensitivity for the three chips mentioned
above and in specific camera configurations is given in Table 2.
| Camera/Chip |
Sensitivitye- / ADU
|
Dark CurrentADU / s |
Temperature°C |
| Photometrics / KAF 1400 |
7.9 |
.002 |
-42 |
| Sony XC-77RRCE / PA-93 |
256.4 |
.043 |
+22 |
| Photometrics / TH 7882 |
90.9 |
.420 |
-37 |
|

