|
with mN
now being the nuclear Bohr magneton:
| |
mN
= eh/ 4pmp =
5.051 x 10-27 J/T |
(6) |
much smaller value because of the ~2000 times more heavier proton mp.
The nuclear g factor, gN, is obtained from a
knowledge of the structure of the nucleus. Interaction with external field
splits the nuclear sublevels due to Zeeman interaction the same way as for
electron spin:
where mI is one of the 2I + 1 projections of the nuclear
spin. Electron-nuclear interaction will depend on the projections of both,
electron and nuclear spins:
| |
Eelectron-nuclear
= A mI ms |
(8) |
where coefficient A, a so-called hyperfine coupling
constant/interaction (hfi), depends not only on the g-values for the electron
and the nucleus but also on the distance between them and their orientation with
respect to the external field (dipole-dipole interaction). In solutions, the
anisotropic part of this interaction averages out because of the fast molecular
rotation. The remaining isotropic part is given by the Fermi contact interaction
in the form:
| |
A = (8p/3)gNmNgemBr(0) |
(9) |
where r(0) = |y(0)|2
is the unpaired electron density at the nucleus. For pure 1s electron on
hydrogen atom, A equals h x 1420 MHz. As a matter of convinience,
hyperfine constants are usually given in Gauss, a = A/gemB.
For example, hydrogen it corresponds to a = 508 G. Summing up all
energies, we arrive at modified Eq. (1):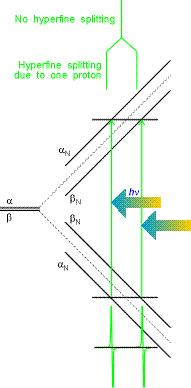
| |
E = gemBms(Bo
+ S aimIi)
- gNmNBomI |
(10) |
You should note two important things:
- the signs in front of ge and
gN
are different because of the opposite charges of the electron and the
proton, causing a spin of the electron to be
higher in energy than b, but
bN spin of the proton to be higher
in energy than aN
- the magnetic field on the electron differs from the Bo
by a integer times ai and the sign of this
cange is opposite for a and b
electron spins
Hydrogen atom example is given on the right. In EPR, allowed transitions
correspond to the change of only ms:
i.e. electronic spin "flips" but the nuclear one remains unchanged.
Thus, in the figure on the right for hydrogen atom, only two transitions can be
observed for a single resonant frequency hn. (This
is a typical mode of EPR signal detection: microwave frequency is kept constant
and magnetic field is varied). These transitions are separated by the
hyperfine constant a (508 G for hydrogen atom). If there are more than
one hydrogens, each of them will
contribute to the change in magnetic field on
the electron.
All
combinations of the nuclear spin projections should be included but (EPR
allowed) transitions only between sublevels with the same configurstions of
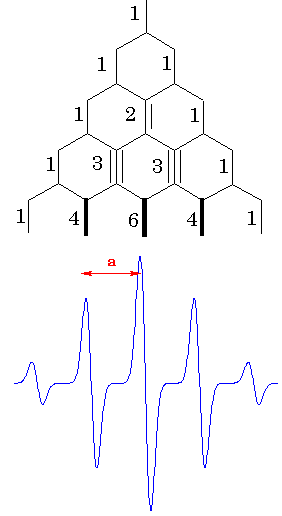
nuclear spins will be realized. For the case of four equivalent protons, a
simple ladder propagation scheme (Figure on the left) illustrates how to
construct the EPR spectrum. Each new step corresponds to one more proton added.
In the first step, two lines appear corresponding to the two different
orientations of mI = -1/2 and mI = +
1/2. In the second step, each line splits into two, corresponding to the two
different orientations of mI = -1/2 and mI
= + 1/2, of the second proton.Since the two protons are equivalent, the
splitting is the same on each step, resulting in three lines of 1:2:1 intesity
ratio. For the four protons, there will be 5 lines with the 1:4:6:4:1 intensity
ratio. Lines with the lengths of these ratio separated by appropriate constants
are called to represent a stick diagram for the radical.
If the spin of the nucleus is greater than 1/2, as in the case of 14N
( I = 1), it splits each of the electronic levels,
a and b, into the 2I + 1 sublevels
resulting in 2I + 1 obeserved lines of equal intensity. In most cases,
one observes a combination of different nuclei with different constants which
sometimes is not as easy to interpret.
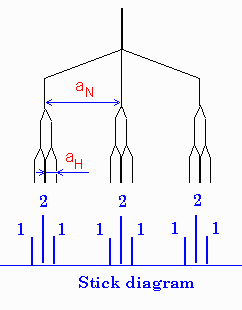
Example
of a radical with two different groups of hfi constants and different nuclei is
shown on the right for a radical with one nitrogen and two equivalent hydrogens
(e.g. NH2).
The magnitude of the hyperfine constants in a radical or radical ion reflects
the extent of s character in its orbital (only s-orbital has nonzero
density at the nucleus). Sometimes it is quite tricky how s -orbital
gets populated. For example, we think of aromatic ion radicals as being purely
p-systems, as you will see for yourselves, there are
substantial hfi constants on there hydrogens. McConnell6 showed that
a aprt of the unpaired p-electron density is
transferred through the C-H sigma bonding electrons to the H nucleus via
exchange interactions. He provided a simple formular which links the aH
on a hydrogen with the unpaired electron spin density on the nearest carbon atom
rp:
The signal intensity in EPR depends on how much absorption of
the microwave power takes place. This value will be the larger the greater is
the difference between populations of the a
and b electron spin states. Following
Boltzmann statistics, the latter can be estimated :
| |
(na- nb)/nb
= e-DE/kT - 1 ~
gmBBo/kBT |
(13) |
a small value for regular X-band EPR spectrometer (9.5 GHz),
which can be substanially increased by lowering the temperatute.
|

