Summary
State-space theory is an elegant way to approach a control problem. A nice aspect is that it naturally seals with multi- variable systems. The theory has given important concepts such as observabilty and reach ability, it has also given several design methods, such as linear quadratic control, loop transfer recovery and pole placement. it has also introduced powerful computational methods based on numerical linear algebra. A severe drawback is that robustness in not dealt with properly. This means that it is possible to formulate control problems which give solutions that have very poor robustness properties. It is easy to avoid the difficulties when we are aware of them, simply by evaluating the robustness of a design and to reduce the requirements until suitable compromise is reached.
3. Fundamental Limitations
It is very useful to determine the performance that can be achieved without sacrificing robustness. Such estimates will be provided in this section. In particular we will consider limitations that arise from poles and zeros in the right half plane and time delays. The results are based on [2]and[11]
Consider a system with the transfer function P(s). factor the transfer function as
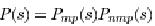
Where is the minimum phase part and is the non-minimum phase part. Let P(s)
Denote the uncertainty in the process transfer function. It is assumed that the factorization is normalized so
that
and the sign is chosen so that Pnmp has negative phase. The achievable bandwidth is characterized by the gain crossover frequency.
4.1 The Crossover Frequency Inequality
We will now derive an inequality for the gain crossover frequency. The loop transfer function is L(s)= P(s)C(s). Requiring that the phase margin is we get.
Where n is the slope of the loop transfer function at the crossover frequency. Equation(28) is also a good
approximation for other controllers because the amplitude curve is typically close to a straight line at the
crossover frequency. The parameter n in (28) is then the slope at the crossover frequency. It follows from
Equations (27) and (28) that the crossover frequency satisfies the inequality
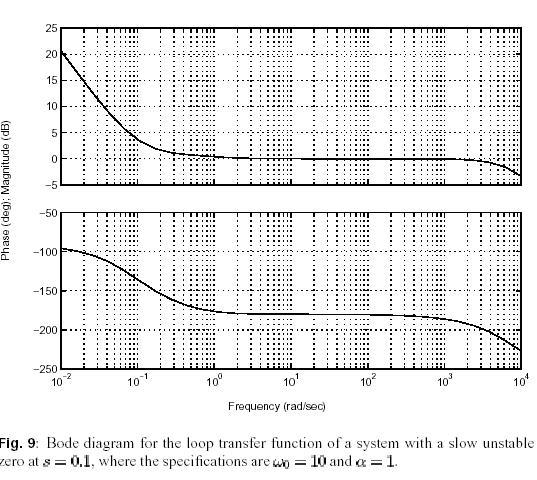
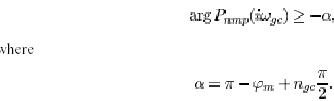This crossover frequency inequality gives the limitations imposed by non-minimum phase factors. A straight forward method to determine the crossover frequencies that can be obtained is to plot the left hand side of Equation (29) and determine when the inequality holds. The following example gives a simple rule of thumb
|
