Graphical solution of 2-var LP's
In this section, we develop a solution approach for LP problems, which is
based on a geometrical representation of the feasible region and the objective
function. In particular, the space to be considered is the n-dimensional
space with each dimension defined by one of the LP variables
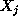
. The objective function will be described in this n-dim space by its
contour plots, i.e., the sets of points that correspond to the same
objective value. To the extent that the proposed approach requires the
visualization of the underlying geometry, it is applicable only for LP's with
upto three variables. Actually, to facilitate the visualization of the concepts
involved, in this section we shall restrict ourselves to the two-dimensional
case, i.e., to LP's with two decision variables. In the next section, we shall
generalize the geometry introduced here for the 2-var case, to the case of LP's
with n decision variables, providing more analytic (algebraic)
characterizations of these concepts and properties.
|